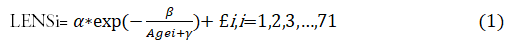Research - (2023) Volume 12, Issue 5
Received: 08-Sep-2023, Manuscript No. IPJBS-23-14081; Editor assigned: 11-Sep-2023, Pre QC No. P-14081; Reviewed: 27-Sep-2023, QC No. Q-14081; Revised: 06-Oct-2023, Manuscript No. R-14081; Published: 16-Oct-2023
Growth curve modelling which is a polular methodological tool due to its flexibility. The presence of many wild rabbits, the Oryctolagus cuniculus, in Australia are of major concern. Researchers were interested to investigate the age of the rabbits. Different types of models, including non-linear models were used. Besides, different types of plots and diagrams for the measures of efficiency were used. Results revealed that dry weight of eye lens of the rabbit has nonlinear relationship with the age of the rabbit. The different posterior summary measures shown that differences between the estimates of the models were shown.
Bayesian analysis, Rabbit, Growth curve
This study is about a Bayesian growth curve model for rabbit animal. Growth curve modeling, which is a popular methodological tool due to its flexibility in simultaneously analyzing both within-animal effects (e.g., assessing change over time for one animal) and between-animal effects (e.g., comparing differences in the change trajectories across animals).
The presence of many wild rabbits, i.e. the Oryctolagus cuniculus, in Australia are of major concern. To have more knowledge on this plague, researchers are interested to determine the age of the rabbits. While before the weight of the rabbit was used as a predictor of the age, the dry weight of the eye lens of the rabbit was proposed as a more reliable method of age determination. Therefore, a study was set up, where they measured the dry weight of the eye lens for free-living wild rabbits of known age [1].
Data description: 72 observations from the slightly modified dataset of rabbit with two variables were given.
Age: Age of rabbit in days a covariate.
Lens: Dry weight of eye lens in milligrams as a response.
Exploratory data analysis: As depicted in Tab.1, the age in days has a mean of 240 and standard deviation of 212.7826 with a minimum and maximum days 2,860 respectively. Whereas that of dry weight of the lens has a mean of 143.37 and standard deviation of 67.16638 in milligrams with minimum and maximum of -2.88, 246.70 respectively [2].
Fig. 1 shows that the growth of dry weight of the eye lens by age (days) are not adequately characterized by a straight line-that is the growth of the rabbit is not linear. Instead, the growth proceed through a number of phases. In the first phase the growth of the animal highly increased, and then after the growth becomes stable, and stable towards a final asymptote. To model growth of the rabbit dry weight in eye lens by age properly, a statistical model must accommodate the nonlinear growth pattern [3].
| Variable | Minimum | Median | Mean | SD | Maximum |
|---|---|---|---|---|---|
| Age | 2.00 | 193.5 | 240.00 | 212.7826 | 860.00 |
| Lens | -2.88 | 177.64 | 143.37 | 67.16638 | 246.70 |
Tab.1: Descriptive statistics for rabbit data.
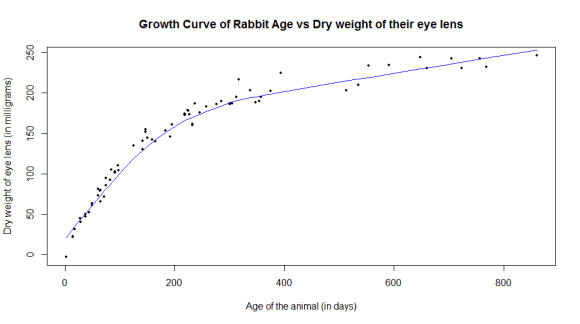
Figure 1: Dry weight of eye lens versus age.
Model fitting 1: Th first nonlinear model Suggested for rabbit dataset is given as below.
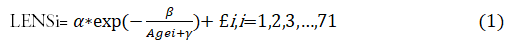
Where, α, β and γ unknown parameters and £ a normally distributed error term with constant variance (σ²). In this model, LENSi is the response measured for the rabbit i=1, ...71 and Agei the age (days) in which dry weight of eye lens were measured i=1, ...71 observation. Before the model was fitted for the final analysis, data was cleaned by removing one observation that have negative value since the dry weight of eye lens could not be negative. Before we remove it, we did the analysis with and without that observation, and we obtained that the estimates have no difference at all. Then the final analysis was done with 71 observations [4].
This model was fitted using vague priors for all model parameters and by taking three chains for each parameter. The convergence of the model was then assessed as presented by history plots after 50000 itp erations with burn in period of 20000 and Brooks-Gelman-Rubin (BGR) Diagnostic as shown in Fig. 2 and 3. The history plots in Fig. 2 show quite a different sampling behavior for the regression parameter than γ parameter. The plots for the regression parameters exhibit slow mixing, but there is rapid mixing for the γ parameter. The posterior distribution is therefore rapidly explored in the direction of γ but slowly explored in the α; β; σ-subspace relatively. However, after forgetting their starting values, the parameters evolves to a relatively stable pattern [5].
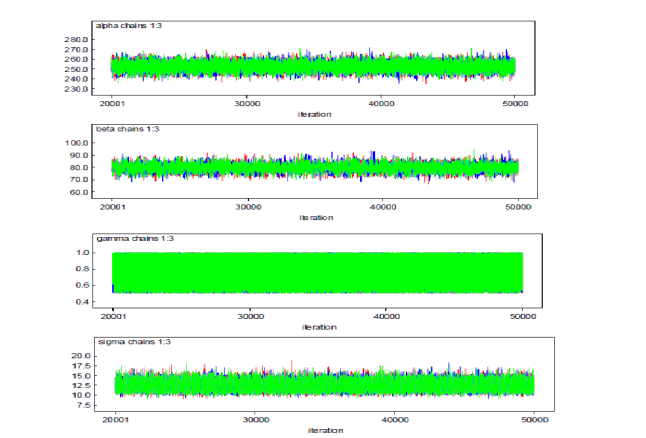
Figure 2: History plot.
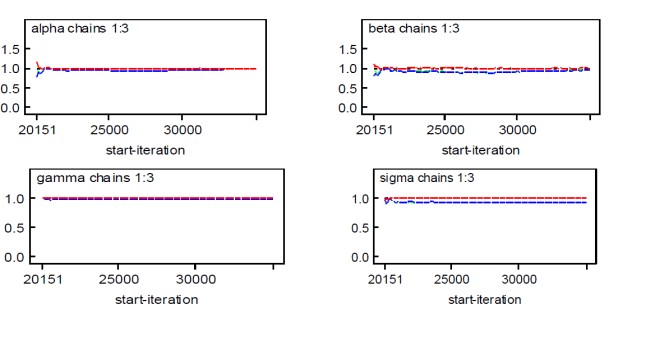
Figure 3: Brooks-Gelman-Rubin diagnostic.
The Gelman-Rubin convergence diagnostic test also shows that the chain converged for all regression parameters as shown in Fig. 3 for all parameters the estimated Potential Scale Reduction Factor (PSRF) are less than 1.1 or 1.2 which implies the chains are mixing well and the posterior distribution were converged.
The efficiency of MCMC method can be measured by the ratio of MC Standard Error (MCSE) to the Standard Deviation (MCSE/SD). MCSE/SD gives the posterior variability due to MCMC simulation (Tab. 2).
| SD | MCSE | MCSE/SD | Effect sample size | |
|---|---|---|---|---|
| Parameters | 3.965 | 0.04365 | 0.0110 | 22000 |
| α | 3.157 | 0.03996 | 0.0126 | 14000 |
| β | 0.1429 | 5.798E-04 | 0.0042 | 20000 |
| ϒ | 1.078 | 0.003781 | 0.0035 | 90000 |
Tab. 2: Measures of efficiency.
Therefore, it is observed from Tab. 2 that the MCSE=SD for parameters alpha and beta are about 1%, and for gamma and sigma are about 0.4% and 0.3% respectively. The result for the parameters alpha and beta implies that the posterior variability due to MCMC simulation in alpha as well as in beta is only 1%, this is suggesting that the MCMC method is efficient. The same is true for the parameters gamma and sigma with 0.4% and 0.3% implying that only 0.4% in gamma and 0.3% in sigma the posterior variability occurred due to MCMC method, which is very small variability and is indicating that the MCMC simulation method is efficient [6].
In addition to that it can also be measured by Effective Sample Size (ESS) and Autocorrelation Function (ACF) as presented. A high value of the ESS in Tab. 2 implies that how the MCMC method was efficient, and also the low autocorrelation presented in Fig. 4 depicted how the MCMC method was efficient as we can see from the plot ACF for all parameters is about zero after lag-50. In conclusion the high ESS and the small ACF implies that MCMC method was efficient.
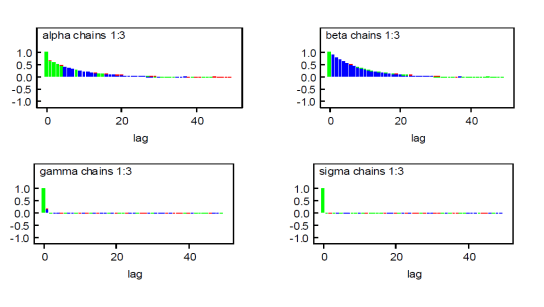
Figure 4: Autocorrelation function.
Assumptions of error terms: The residual plot in Fig. 5(a) seems to indicate that the residuals and the fitted values are in a hoT moscedastic variation with normally distributed errors. A Q-Q plot in Fig. 5(b) that plotted for two sets of quantiles against one another shows that the quantiles came from the same normal distributions [7].
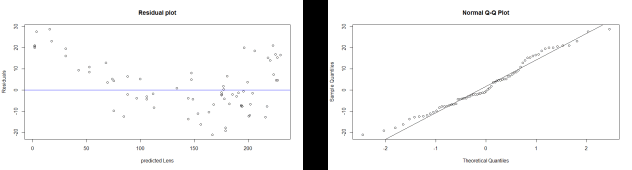
Figure 5: Assumption for error term.
Moreover, Posterior Predictive Checks (PPC) are used only as measures of discrepancy between the model and the data in order to identify poorly fitted models (model adequacy) and not for model comparison and inference. As the aim of PPC is to assess the systematic discrepancies between the observed data and (hypothetical) replicated data generated from the fitted model, P-values for Skewness and kurtosis of test statistic and discrepancy measures were given here. As it was observed from the Tab. 3, the p-values are higher than 5% significance level except for the Skewness test. Although Skewness test indicates that there is no goodness of fit, this was not confirmed by the kurtosis measure of discrepancy. Therefore, the model fits the data well [8].
| Test | PTskew | PDskew | PTkurt | PDkurt |
|---|---|---|---|---|
| Estimate | 0.00012 | 0.07850 | 0.99700 | 0.60000 |
Tab. 3: Posterior Predictive Checks (PPC) for checking model adequacy.
The histogram of the kurtosis in Fig. 6 (a) seems that the concentration of the observation is too much at the center we can call it Leptokurtic. But the kurtosis discrepancy measure in Fig. 6 (b) seems the distribution is symmetric and normal. But the histogram in Fig. 6 (c) is moderately skewed left, the left tail is longer and most of the distribution is at the right. Also the measure of Skewness discrepancy measure seems the distribution of the data is to one direction as we can see from the Fig. 6 (d). From this we can conclude that the distribution of the observation by measure of kurtosis discrepancy seems normal.
Figure 6: Posterior predictive hecks.
For checking the outlying observations, index plot of icpo (inverse conditional predictive ordinate) was used (Fig. 7). Since a small value of iCPO (larger value of CPO) implies a better fit of the model to a single observation, and large iCPO valus (low CPO values) suggested that observation is an outlier and an influential observation. Due to the face that Inverse-CPO’s (ICPO’s) larger than 40 can be considered as possible outliers, and higher than 70 as extreme values, the index of iCPO pointed that there seems five possible outlying regions, i.e. regions 6, 36, 44, 55 and 65 might be considered as outlying. These regions in turn considered of considerable observations, but possibly region 6 is the extreme region with about 5 observations [9].
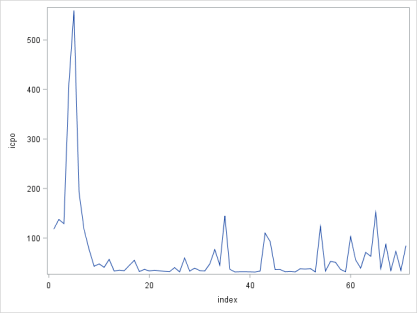
Figure 7: Index plot of iCPO.
Model fitting 2: The second nonlinear model assumed for the Rabbit data set is given as below.
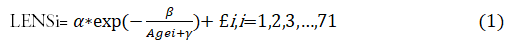
with α, β and γ unknown parameters and £ a normally distributed error term with constant variance (σ²). In this model LENS i is the response measured for the rabbit i = 1; :::71 and Age i the age (days) in which dry weight of eye lens were measured i = 1; :::71 observation.
In order to select the best one from models (1) and, Deviance Information Criteria (DIC) was used (Tab. 4).
| Model | DIC |
|---|---|
| Model I | 561.768 |
| Model II | 678.096 |
Tab. 4: The two models and their respective DIC values.
As a very roughly rule of thumb, differences of more than 10 might definitely rule out the model with the higher DIC. As it is observed in Tab. 4, model 1 is taken as the best since its DIC value is smaller than that of model 2 and the difference is clearly visible that is more than 10 (Tab. 5).
| Node | Mean | SD | MC error | 2.50% | Median | 97.50% | Start | Sample |
|---|---|---|---|---|---|---|---|---|
Model I |
||||||||
| α | 252.4 | 4.001 | 0.045 | 244.7 | 252.4 | 260.4 | 20001 | 90000 |
| β | 79.69 | 3.189 | 0.042 | 73.58 | 79.63 | 86.14 | 20001 | 90000 |
| ϒ | 0.777 | 0.142 | 5.42E-4 | 0.518 | 0.790 | 0.991 | 20001 | 90000 |
| σ | 12.43 | 1.078 | 0.004 | 10.54 | 12.35 | 14.76 | 20001 | 90000 |
Model II |
||||||||
| α | 4.507 | 0.039 | 6.80E-4 | 4.43 | 4.507 | 4.586 | 20001 | 90000 |
| β | 115.9 | 15.88 | 0.273 | 87.48 | 114.9 | 150 | 20001 | 90000 |
| ϒ | 0.742 | 0.144 | 5.21E-4 | 0.512 | 0.738 | 0.987 | 20001 | 90000 |
| σ | 28.19 | 2.433 | 0.009 | 23.89 | 28.03 | 33.39 | 20001 | 90000 |
Tab. 5: Posterior summary measures of model 1 and model 2.
It is depicted from Tab. 5 that the estimated values (mean) and median for α and σ are higher in model I than in model II, but for β they are higher in model II. The credibility equal tail interval for respective parameter gives the domain (interval) of the posterior probability of that parameter estimate. The MC errors are small (smaller than 5% SD) in all parameters of both models. 20001 and 90000 implies that 20000 burn-in iterations and 90000 extra iterations were performed.
To compare the estimated curves of the two models, Fig. 8 was given below.
Fig. 8 indicated that the fitted average curve for model I seems to have the better fit as compared to that of model II.
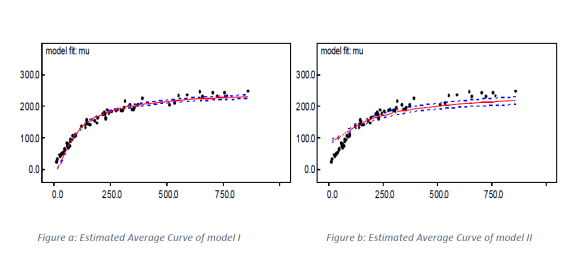
Figure 8: Estimated average curves of the two models.
In order to have some insight in to the data, descriptive statistics using tabular and graphical description was done. From the growth curve it was depicted that the dry weight of eye lens has a nonlinear relationship with age. Observing this, two different nonlinear models were fitted separately using vague priors for all parameters, and taking three chains their convergence were assessed. Eventually, as the MC error of each parameter was less than 5% of its respective standard deviation, well convergence was observed. Goodness of fit test was done using posterior predictive checks, and was shown that the model fitted the data well. Moreover, conditional predictive ordinate was used to check outlying observations, and some outlying observations were observed. The two models were compared using DIC, and model I was chosen as the best model as it has small DIC. As well, the posterior summary measures for all the model parameters of models were assessed, and in some case, differences between the estimates of the two models were revealed. Choosing model I as the best using DIC was also confirmed by the estimated average curves.
[Crossref] [Google Scholar] [PubMed]
[Crossref] [GoogleScholar] [PubMed]
[Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
[Crossref] [Google Scholar] [PubMed]
