Archivos de Medicina

Keywords

Math; Fractals; Hematology; Erythrocyte; Morphophysiology

Introducción

La regularidad las figuras geométricas es caracterizada mediante reglas euclidianas como son la longitud, área y el volumen. Dichas reglas son propiedades y relaciones geométricas de las figuras regulares en el plano o el espacio. No obstante, se ha demostrado que la irregularidad de algunas figuras u objetos no es posible caracterizarla mediante la geometría euclidiana, dando origen a una nueva rama de la matemática denominada geometría fractal. El objeto caracterizado mediante esta geometría se denomina fractal, y su irregularidad cuantificada mediante la dimensión fractal [1-3]. Debido a los diferentes tipos de fractales, cada uno de ellos cuenta con un método matemático que permite calcular la dimensión fractal. Por ejemplo el fractal salvaje se caracteriza por la superposición de sus partes, la autosimilitud y la irregularidad es calculada mediante el método de Box-Counting [4].

En la literatura médica, los glóbulos rojos se caracterizan por la capacidad que tienen para someterse a grandes deformaciones pasivas durante el paso repetido a través de los capilares estrechos de la microvasculatura, a lo largo de su vida útil de 120 días [5]. Rand y Burton, desarrollaron la técnica de aspiración micropipeta para medir la "rigidez" de la membrana, en relación a la regulación de la funcionalidad de los glóbulos rojos [6]. El eritrocito normal se caracteriza por presentar una forma bicóncava y de disco cóncavo, además se le atribuye una forma redonda cuyo diámetro varía entre 7 μm y 9 μm. Al observar a través de microscopio de luz las variaciones en las características anteriormente mencionadas, se considera la muestra como anormal y es asociada a una posible enfermedad [7]. Entre estas variaciones se encuentra el equinocito su nombre se deriva de la palabra erizo de mar, en vista que este presenta espículas cortas con extremos romos, distribuidas regularmente por toda la superficie de la célula [7].

El estudio de la morfología de los hematíes se usa como método para el diagnóstico de numerosas hemopatías. La cuantificación del factor de forma en la deformabilidad eritrocitaria se realiza mediante la relación de superficie (S) - volumen (V). El resultado de S/V, es considerado también como un índice que evalúa la incidencia del factor de forma en la deformabilidad eritrocitaria. Los equinocitos se presentan en muestras de extendidos de sangre periférica de pacientes con anemia hemolítica aguda [8], con enfermedad renal crónica [9,10], con quemaduras severas [11], y en pacientes que han sido transfundidos [12], debido a que en la sangre de banco se forman equinocitos en cantidad proporcional con la edad de la sangre, conocidos como esferoequinocitos [13].

En cambio, los estudios realizados en el contexto de teorías físicas y matemáticas han logrado caracterizar de manera óptima las alteraciones de los eritrocitos, aplicando para ello las nociones de la geometría fractal y euclidiana de manera simultánea [14-16]. Los eritrocitos normales y sus alteraciones fueron caracterizados por vez primera en el contexto de la geometría fractal; logrando cuantificar la irregularidad de las alteraciones de los eritrocitos de manera objetiva y reproducible con el método de Box Counting [14]. Esta metodología fue posteriormente refinada mediante la aplicación conjunta de la geometría euclidiana y fractal, logrando evaluar de forma más precisa las irregularidades de otras muestras de extendido de sangre periférica. Esto fue posible, mediante las proporciones entre la superficie y el borde de la estructura del eritrocito, estableciendo un orden matemático que diferencia las distintas alteraciones de los eritrocitos [15]. Como resultado de estas dos metodologías, se realizó una simulación teórica para las distintas estructuras eritrocitarias, la cual facilita un seguimiento de la evolución de estas alteraciones morfológicas en el tiempo [16].

El propósito de la presente investigación es aplicar las metodologías previamente desarrolladas para caracterizar la estructura de los equinocitos, mediante el método de Box Counting en el contexto de la geometría fractal [14-16].

Metodología

Método de box counting: Método matemático para evaluar el grado de irregularidad y la dimensión fractal de un objeto. Siendo K: el grado de partición de la cuadrícula, N: es el número de espacios que contiene el contorno del objeto y D: la dimensión fractal.

Rejillas cuadros pequeños (Kp) y cuadros grandes (Kg): consiste en dos cuadriculas con dimensiones de 5 × 5 y 10 × 10 pixeles.

Superficie en píxeles de las regiones de los equinocitos: número de píxeles que tocan el interior o el borde de la imagen medida.

Procedimiento

Del Laboratorio de referencia en Morfología Hematológica, se tomaron diferentes tipos de muestras de sangre, cuyos extendidos de sangre periférica presentaba equinocitos, los cuales fueron evaluados por el especialista del laboratorio según los parámetros convencionales. Las muestras de sangre fueron observadas en extendidos tratados con colorante Romanowsky, con un aumento de 10 × por 100 × a través de un microscopio Carl Zeiss y las imágenes fueron tomadas por una Cámara de microscopio digital.

Para que el software reconozca las imágenes de extendido de sangre periférica, estas fueron editadas en Microsoft Office Professional Plus 2010, dejando la dimensión de cada una de ellas en 448 × 336 pixeles. Posteriormente, y según la imagen del extendido de sangre periférica fueron seleccionados entre uno a tres equinocitos, para ser delineado su contorno tal y como se puede ver en la Figura 1. Luego se superpusieron las dos rejillas (ver definiciones), para evaluar mediante el método de Box Counting el espacio ocupado por los equinocitos, así como su dimensión fractal. Estas dos rejillas fueron escogidas porque sus escalas permitieron evidenciar diferencias entre normalidad y enfermedad en las dos metodologías previamente desarrolladas [14-16]. En vista que con la rejilla Kg no se logró cuantificar con mayor precisión las irregularidades de los equinocitos, lo que sí pudo hacer con la rejilla Kp (Figura 1), los valores calculados con esta rejilla no fueron considerados para realizar el análisis.

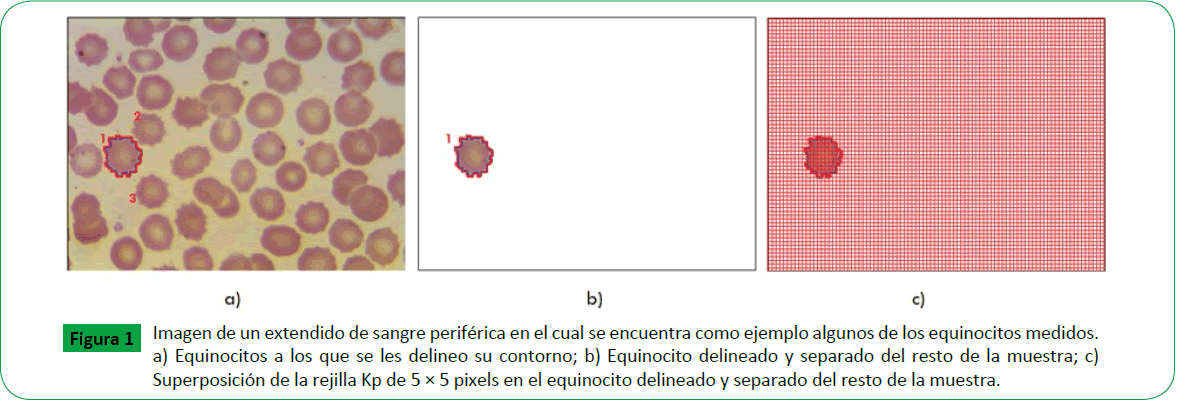
Figure 1: Coalescing pustules, erythematous papules and plaques on the lateral side of the trunk.

Finalmente, para establecer los valores que permiten establecer igualdades o diferencias entre los equinocitos, se calculó las proporciones, es decir, el cociente entre los valores de la superficie y la rejilla Kp de los equinocitos seleccionados para el estudio.

Resultados

Los valores ocupados por los equinocitos con la rejilla Kp variaron entre 37 y 45. La dimensión fractal los equinocitos variaron entre 0,96 y 1,23. La superficie de los equinocitos variaron entre 1280 y 1977 y la proporción entre la superficie y la rejilla Kp varió entre 34,59 y 46,50 (Tabla 1).

Equinocito	1	2	3	4	5	6	7	8	9	10
Kp	37	43	37	37	37	45	43	45	42	40
Df	0,96	1,10	1,04	1,04	1,12	1,17	0,97	1,17	1,00	1,23
S	1529	1552	1412	1385	1280	1634	1737	1977	1628	1860
S/Kp	41,32	36,09	38,16	37,43	34,59	36,31	40,4	43,93	38,76	46,50

Tabla 1: Medidas de 10 de los 20 equinocitos tomados de la sangre periférica. Kp: es el número de cuadros ocupados por la rejilla de 5 × 5 pixeles. Df: es la dimensión fractal; S: superficie. S/Kp: proporción entre la superficie y el número ocupados con la rejilla Kp.

Discusión

Este es el primer trabajo en el que caracteriza la irregularidad de los equinocitos en el contexto de la geometría fractal. Para ello fue evaluado el contorno y la superficie del equinocito mediante el método de Box Counting. Se estableció un orden matemático a partir de valores hallados que permite hacer distinciones entre los espacios ocupados por los equinocitos. Como consecuencia de esto, la metodología contribuye a realizar caracterizaciones más precisas de los equinocitos, no por el número de espículas cortas con extremos romos comúnmente observadas en los equinocitos, sino por los valores matemáticos que evalúan su grado de irregularidad.

A partir de las características morfológica particulares de los equinocitos se establecen distinciones entre los diferentes tipos de eritrocitos con el propósito de clasificarlos. Cabe decir que el presente estudio en cambio, aporta un nuevo sistema de medida que permite caracterizar la estructura del eritrocito aun cuando este no cumpla con todas las características morfológicas de un equinocito, aplicando para ello una misma metodología. La presente metodología, evaluó la irregularidad del equinocito independiente del tamaño, color y la cantidad de espículas cortas con extremos romos, los cuales son considerados en otros estudios desarrollados en el contexto de la geometría fractal y redes neurales [17].

De igual manera, las estructuras eritrocitarias normales y anormales, evaluadas previamente a partir de la metodología desarrollada Rodríguez et al., evidencian que tan apropiado resulta caracterizar las estructuras eritrocitarias desde la noción de la geometría fractal, logrando como resultado medidas objetivas y reproducibles independientes de las características morfológicas atribuidas a las alteraciones de los eritrocitos, desde el ámbito clínico [14-16]. Debido a este tipo de estudio, recientemente se realizó una generalización de todas las posibles trayectorias de las alteraciones de los eritrocitos, con base en los valores de los espacios ocupados por el borde y superficie de los eritrocitos normales y equinocitos [9]. Así mismo, la metodología reveló como ambas geometrías pueden caracterizar la estructura eritrocitaria, mediante la aplicación correcta de las nociones de irregularidad, área y superficie.

La geometría euclidiana en su dimensión física da cuenta de las propiedades espaciales de los objetos físicos, así como de sus representaciones modelando el espacio que nos rodea a partir de ellas [17]. Es por ello que los eritrocitos y las distintas alteraciones en su forma, son descritos mediante reglas euclidianas, que relacionan los eritrocitos con figuras que tienen por forma un anillo o disco cóncavo, esfera y elipse [6,18,19]. Como resultado es esto, las características particulares de los eritrocitos, resultan a menudo insuficientes para dar cuenta de las variaciones de un eritrocito, en pleno comienzo y evolución de la infección de la malaria [20] u otra patología, así mismo, para evaluar el nivel de efectividad y adversidades de un tratamiento terapéutico [21]; por ejemplo cuando el tratamiento es realizado por radiación de rayos X [22]. En cambio, estudios realizados desde el contexto de la geometría fractal han evidenciado que los valores de la dimensión fractal de los agregados de sedimentación, generan un modelo matemático que permite predecir el comportamiento de los eritrocitos [23].

Espacio geométrico de Box Counting, proporciona las herramientas necesarias para establecer relaciones armónicas matemáticas entre el objeto medido y el espacio ocupado por el objeto, permitiendo caracterizar otras estructuras como son la arterial, ventricular y en células de cuello uterino, entre otras [24-26]. La presente metodología se puede entender, considerando el estudio desde el ámbito acausal, el obedece a la noción de ventanas temporales, cuya finalidad se centra en el establecimiento de órdenes matemáticos implícito en la estructura del equinocito independientemente de cualquier análisis poblacional, siendo posible contrastarlos en cada caso particular.

A la luz de estos nuevos métodos de investigación, se han desarrollado nuevas metodologías de aplicación clínica, que contribuyen a dar soluciones en otros ámbitos de la medicina como son en el estudio de la dinámica cardiaca de adulto [27], fetal [28], neonatal [29], logrando recientemente una metodología que predice casos de mortalidad [30]. En epidemiología se han desarrollado predicciones de brotes de malaria en 820 municipios de Colombia en rangos de tres semanas, con un 99,86% de efectividad [31]. También se han desarrollado métodos predictivos en inmunología [32], biología molecular [33] e infectología [34,35]. En consecuencia, estas metodologías evidencian la aplicabilidad práctica que tiene el uso de las mismas en las diferentes ramas de la medicina.

Conclusiones

Los principios matemáticos de la geometría fractal que fundamentan la presente metodología, contribuyen a realizar una descripción y cuantificación más precisa de los cambios externos del equinocito.

Agradecimientos

Agradecemos a los docentes de la Escuela de Ciencias Básicas, Tecnología e Ingeniería de la Universidad Nacional Abierta y A distancia.

Este artículo es producto del proyecto: Evaluación física y matemática de variables hemodinámicas de pacientes de la Unidad de Cuidados Intensivos fundamentada en la geometría fractal y los sistemas dinámicos: Cuantificaciones de aplicación clínica en 14 horas; desarrollado en el Centro de Investigaciones de Clínica del Country, en alianza con la Universidad Militar Nueva Granada.

Agradecemos a la Universidad Militar Nueva Granada, por su apoyo a nuestras investigaciones. Especialmente a la Vicerrectoría de Investigaciones y la Facultad de Medicina. Extendemos un agradecimiento especial a la Dra. Nydia Alexandra Rojas, Directora de Investigaciones de la Facultad de Medicina, al Dr. Jorge Luque, Decano de la Facultad de Medicina, a la Dra. Yanneth Méndez, Vicerrectora académica y a la Ing. Marcela Iregui, Vicerrectora de Investigaciones.

Agradecemos también, al Centro de Investigaciones de la Clínica del Country, en especial a los Doctores Tito Tulio Roa, Director de Educación Médica, Jorge Ospina, Director Médico, y Alfonso Correa, Director del Centro de Investigaciones; a la Doctora del Centro Adriana Lizbeth Ortiz, epidemióloga, y a la enfermera Silvia Ortiz, por el apoyo a nuestras investigaciones.

Dedicatoria

A los hijos del primer autor.

18740

References

1. Mandelbrot B (1967) Howlong Is the coast of britain? statistical self-similarity and fractional dimension. Science 156: 636-638.
2. Mandelbrot B (2000) Árbolesjerárquicos o de clasificación, y la dimensión. En: Los objetosfractales. Barcelona: TusquetsEds S.A. 161-166.
3. Mandelbrot B (1972) Thefractal geometry of nature. San Francisco: Freeman Ed, pp: 341-348.
4. Peitgen H, Jürgens H, Saupe D (1992) Thebox-counting dimension en: Chaos and chaos and fractals: New frontiers of science. New York: Springer-Verlag. pp: 655-768.
5. Narla M, Gallagher P (2008) Red cell membrane: past, present, and future. Blood 112: 3939-3948.
6. Rand RP, Burton AC (1964) Mechanical properties of the red cell membrane. I. membrane stiffness and intracellular pressure. Biophys J 4:115-135.
7. Campuzano G (2008)Utilidadclínicadelextendido de sangreperiférica: los eritrocitos. Medicina&laboratorio14: 311-313.
8. Jacob HS, Amsden T (1971) Acutehemolyticanemia with rigid red cells in hypophosphatemia. N Engl J Med 285: 1446-1450.
9. Agroyannis B, Kopelias I, Fourtounas C, Paraskevopoulos A, Tzanatos H, Dalamangas A, et al. (2001) Relation between echinocytosis and erythrocyte calcium content in hemodialyzed uremic patients. Artif Organs 25: 486-490.
10. Sakthivel R, Farooq SM, Kalaiselvi P, Varalakshmi P (2007) Investigation on the early events of apoptosis in senescent erythrocytes with special emphasis on intracellular free calcium and loss of phospholipid asymmetry in chronic renal failure. ClinChimActa 382: 1-7.
11. Harlan WR, Shaw WA, Zelkowitz M (1976) Echinocytes and acquired deficiency of plasma lipoproteins in burned patients. Arch Intern Med 136: 71-76.
12. Laczko J, Feo CJ, Phillips W (1979) Discocyte-echinocyte reversibility in blood stored in CPD over a period of 56 days. Transfusion 19: 379-388.
13. Bain BJ (2006) Blood cells. A practical guide. (4th edn.), Malden, Massachusetts USA: Blackwell Publishing.
14. Rodríguez J, Correa C, Prieto S, Ospino B, Bernal P, et al. (2008) Caracterizacióngeométrica de los glóbulosrojos. Diferenciación de muestrasnormales y patológicas. Rev CiencSalud 6: 47-56.
15. Correa C, Rodríguez J, Prieto S, Álvarez L, Ospino B, et al. (2012) Geometric diagnosis of erythrocyte morphophysiology. J Med MedSci 3: 715-720.
16. Rodríguez J,Prieto S, Correa S, Mejía M,Ospino B, et al. (2014) Simulación de estructuraseritrocitarias con base en la geometría fractal y euclidiana. Arch Med (Manizales) 14: 276-284.
17. Camargo L, Acosta M (2012) La geometría, suenseñanza y suaprendizaje. Rev FacCiencTecnol 32: 4-8.
18. Pinzón R, Garavito G, Hata Y, Artega L, García JD (2004) Desarrollo de un sistema de análisisautomático de imágenes de ExtendidoSanguíneos. En memoriasdelcongresoespañolde la sociedadde ingenieríabiomédicapp: 45-59.
19. Diez-Silva M, Dao M, Jongyoon H, Chwee-Teck L, Suresh S (2010) Shape and biomechanical characteristics of human red blood cells in health and disease. MRS Bull 35: 382-388.
20. Thurston H, Karl S, Malcolm M, Terrie, Pradipsinh R (2012) Estimating Physical splenic filtration of plasmodium falciparum Infected red blood cells in malaria patients. Cell Microbiol 14: 1880-1891.
21. Zuk A, Targosz M, Szymonski M (2011) Effect of selected drugs used in asthma treatment on morphology and elastic properties of red blood cells. Int J Nanomedicine 6: 249-257.
22. Xu D, Peng M, Zhang Z, Dong G, Zhang Y, et al. (2012) Study of damage to red blood cells exposed to different doses of γ-ray irradiation. Blood Transfus. 10: 321-330.
23. Tang P, Greenwood J, Raper JA (2002) A model to describe the settling behavior of fractal aggregates. J Colloid Interface Sci 247:210-219.
24. Rodriguez J, Prieto S, Correa C, Bernal P, Puerta G, et al. (2010) Theoretical generalization of normal and sick coronary arteries with fractal dimensions and the arterial intrinsic mathematical harmony. BMC Medical Physics 10:1-6.
25. Rodríguez J, Prieto S, Correa C, Bernal P, Álvarez L, et al. (2012) Diagnóstico fractal del ventriculogramacardiacoizquierdo. Geometría fractal delventriculogramadurante la dinámicacardiaca. Rev ColombCardiol 19:18-24.
26. Velásquez J, Prieto S, Catalina C, Dominguez D, Cardona DM, et al. (2015) Geometrical nuclear diagnosis and total paths of cervical cell evolution from normality to cancer. J Cancer Res Ther11: 98-104.
27. Rodríguez J, Prieto S, Domínguez D, Melo M, Mendoza F, et al. (2013) Mathematical-physical prediction of cardiac dynamics using the proportional entropy of dynamic systems. J Med MedSci 4:370-381.
28. Rodríguez J (2012) Nuevo diagnósticofísico y matemático de la monitoriafetal: predicción de aplicaciónclínica. MomentoRevista de Física 44: 49-65.
29. Rodríguez J, Prieto S, Flórez M, Alarcón C, López R, et al. (2014) Physical-mathematical diagnosis of cardiac dynamic on neonatal sepsis: predictions of clinical application. JMedMedSci 5: 102-108.
30. Rodríguez J (2015) Dynamical systems applied to dynamic variables of patients from the intensive care unit (ICU): Physical and mathematical mortality predictions on ICU. J Med MedSci 6:209-220.
31. Rodríguez J (2010) Métodopara la predicción de la dinámica temporal de la malaria en los municipios de Colombia. Rev PanamSaludPública. 27:211-218.
32. Rodríguez J, Bernal P, Álvarez L, Pabón S, Ibáñez S, Chapuel N, et al (2010) Predicción de unión de péptidos de MSP-1 y EBA-140 de plasmodium falciparum al HLA clase II Probabilidad, combinatoria y entropíaaplicadas a secuenciaspeptídicas. Inmunología 29:91-99.
33. Rodríguez J, Bernal P, Prieto S, Correa C (2010) Teoría de péptidos de altaunión de malaria al glóbulorojo.Prediccionesteóricas de nuevospéptidos de unión y mutacionesteóricaspredictivas de aminoácidoscríticos.Inmunología29:7-19.
34. Rodríguez J, Prieto S, Correa C, Forero M, Pérez C, et al. (2013) Teoría de conjuntosaplicada al recuento de linfocitos y leucocitos: predicción de linfocitos T CD4 de pacientes con VIH/SIDA. Inmunología 32: 50-56.
35. Rodríguez J, Prieto S, Correa C, Mora J, Bravo J, et al. (2013) Predictions of CD4 lymphocytes’ count in HIV patients from complete blood count. BMC Medical Physics. BMC Medical Physics 13:3.