Archivos de Medicina

Keywords

alometric equations, darwinism, embryogenic growth, fractals, invagination, proteins

Introducción

El ser humano se ha venido considerando y aún se considera como el animal histórico por excelencia. Para nosotros, este concepto debe ampliarse a todos los objetos del universo. En este sentido, los más próximos a nosotros, y, en particular, los que constituyen nuestro hábitat, llamados inertes y vivos, poseen una historia común y comparten características comunes, y otras que son muy diferentes. La unidad de la vida es la célula, un sistema abierto que para su sostenimiento y mantenimiento (reproducción) intercambia con el ambiente a través de su superficie limitante materia y/o energía. Su asociación origina los seres pluricelulares. La conveniencia de mantener en un valor adecuado las superficies de intercambio, determina muchas de sus características, en particular la forma del individuo [1-4].

La evolución de los seres vivos, el darwinismo [5], contempla tanto la historia de las especies, desde las células primitivas, en la filogenia, como la historia de los individuos, en la ontogenia-embriogenia.

A pesar de tratarse de fenómenos muy interesantes no han suscitado, sin embargo, la atención que, creemos, merecen; incluso los conceptos básicos subyacentes son conocidos solamente por los naturalistas.

Dichos fenómenos consisten en una serie de transformaciones que se inician con la aparición del zigoto, que resulta de la fecundación del óvulo por el espermatozoide [6]. La división celular de este zigoto, mediante la cual aumenta la población de células descendientes, pasa por una serie de etapas (mórula, gástrula, blástula,...) hasta alcanzar poblaciones con un número de descendientes del orden de 1013, correspondientes “grosso modo” al individuo formado.

El estudio de este proceso pertenece a la embriología, siendo la humana la que, por diversas razones, ha merecido la mayor atención por parte de médicos y/o naturalistas. Tal y como suele ser conocida [7-10], consiste en una descripción pormenorizada de ciertas características asociadas al embrión primero y al feto después a lo largo de su desarrollo, descripción que proporciona información pero no explicación y/o interpretación, dentro de un marco conceptualmente consistente. En lo esencial, esta fenomenología podría parangonarse con la utilizada en la era precientífica.

Resultados y discusión

En primer lugar, se admite que los objetos materiales, cuyo conjunto constituye el universo se han formado gracias a la acción de ciertas fuerzas que han actuado a lo largo de las diferentes entidades que fueron apareciendo hasta llegar al momento actual.

Inicialmente, el universo consistió en un conjunto de partículas y radiación (Figura 1), aceptándose que las fuerzas se deben al intercambio de partículas, como ocurre por ejemplo en el juego del ping-pong, en el que la pelota que va y viene de un jugador al otro, es la que en realidad los mantiene unidos, ocurriendo lo mismo en el caso del tenis.

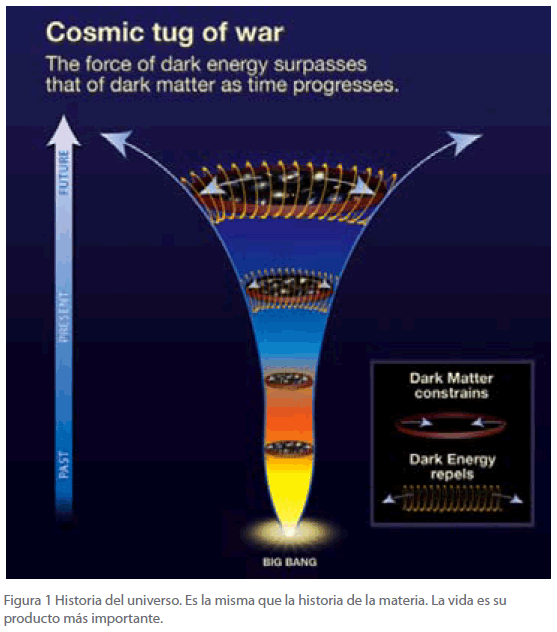
Figura 1 Historia del universo. Es la misma que la historia de la materia. La vida es su producto más importante.

Las fuerzas son las siguientes (Figura 2) [11-16]:

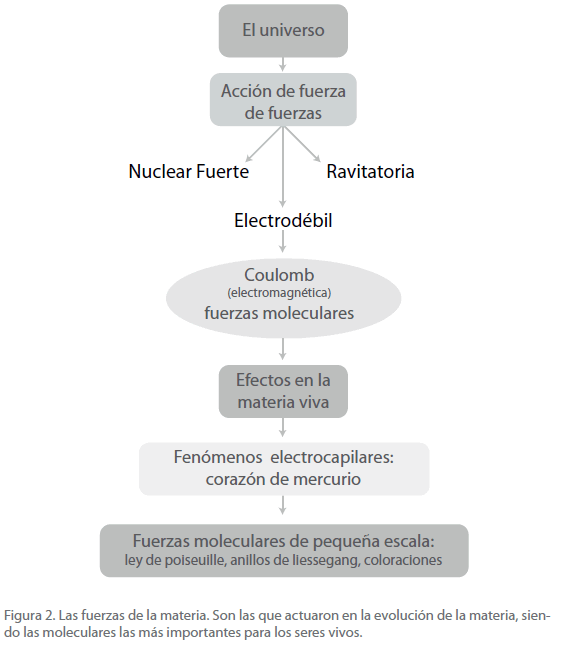
Figura 2. Las fuerzas de la materia. Son las que actuaron en la evolución de la materia, siendo las moleculares las más importantes para los seres vivos.

La nuclear fuerte que mantiene unidos los quarks (principalmente los u y d) en los nucleones, de los cuales, los más importantes para nosotros son el protón y el neutrón.

La electrodébil, que incluye la de Coulomb, llamada electromagnética. Esta es la fuerza más importante en el contexto de este trabajo y de ella nos ocuparemos con detalle más adelante.

La gravitatoria que domina la dinámica del universo, desde las grandes masas, que incluyen supercúmulos y cúmulos de galaxias, estrellas, hasta los planetas, satélites y grandes meteoritos [17].

Se considera, a continuación, el papel desempeñado por las fuerzas en las diferentes entidades del universo y en particular a las responsables de la existencia de la materia viva.

En los átomos, moléculas y cuerpos de nuestro entorno más inmediato, las fuerzas nucleares se hallan secuestradas debido al apantallamiento ejercido por los electrones negativos (efecto Faraday). El papel de los núcleos consiste en proporcionar el sostén necesario para que las fuerzas electrodébiles puedan ejercer su función, y en particular, la fuerza de Coulomb. Recordemos que esta fuerza es formalmente idéntica a la fuerza gravitatoria, solo que se refiere a las cargas.

Para nosotros las fuerzas llamadas generalmente moleculares (así llamadas porque se ejercen entre los dipolos moleculares) son las más importantes en la materia viva y derivan de la fuerza de Coulomb. En el caso de la molécula de agua ocurre que al ser asimétrica, no coinciden las cargas positivas con las negativas y se tiene un dipolo. Al aplicar a los dipolos la ley de Coulomb, se obtiene un resultado diferente del caso en que las cargas fuesen puntuales. Una gran variedad de fenómenos están relacionados con la presencia de dipolos en las moléculas, como los electrocapilares, algunos tan llamativos como el llamado “corazón de mercurio”; en las oscilaciones del cual intervienen la tensión superficial del mercurio y la adsorción sobre su superficie de los iones existentes en una disolución acuosa de dicromato potásico.

Las moléculas más importantes en los procesos vitales son las proteínas [18-22], que son polímeros de aminoácidos y se presentan en disolución acuosa generalmente como cadenas plegadas. Estas moléculas están cubiertas por un manto de moléculas de agua gracias a los puentes de hidrógeno existentes tanto en ramificaciones de la molécula como en la propia molécula de agua. Una molécula de las dimensiones de una proteína exhibe una superficie de grupos químicos y de los correspondientes electrones, es decir, se trata de una superficie eléctrica, en la que un electrón exterior puede desplazarse como lo hace un objeto masivo sobre una superficie accidentada. El proceso de la catálisis se debe a que alguno de estos accidentes puede poseer una forma parecida a la de otra molécula exterior, como si se tratara de una llave y la correspondiente cerradura, con el resultado de facilitar enormemente la reacción correspondiente. Los procesos vitales consisten en la repetición de reacciones entre proteínas, en las que el electrón es el principal protagonista. La enorme variedad de proteínas explica la gran diversidad de los procesos vitales. Por otra parte es conocido que las proteínas son producidas mediante una serie de procesos moleculares en los que intervienen las moléculas ADN y ARN [23,24] que forman los genes característicos de cada especie. Dicho con otras palabras, las proteínas del juego de la vida en una determinada especie deben ser las mismas que las proporcionadas por la maquinaria citada, maquinaria que utiliza ciertos y determinados genes. El mantenimiento de este acoplamiento podría estar relacionado con la expresión genética.

Los mecanismos citados, que podrían parecer cosa de magia, no son exclusivos de la materia viva, sino el resultado de ciertas restricciones impuestas por el medio.

La hipótesis de trabajo consistió en comprobar que el comportamiento de la materia viva es susceptible de ser descrito cuantitativamente de la misma o parecida manera a como se realiza con la materia ordinaria (inerte).

Las fuerzas gravitatorias formaron la Tierra y modelaron su superficie transportando sus materiales. Podemos decir que prepararon un asentamiento adecuado para la materia viva.

Brevemente, los acontecimientos que ocurrieron en la formación de la Tierra fueron los siguientes (Figura 3).

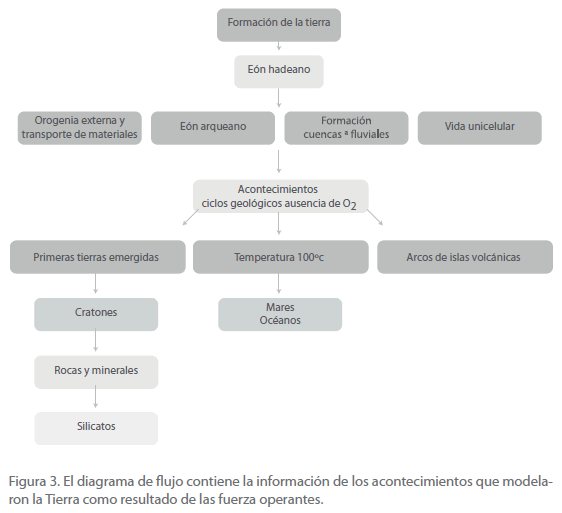
Figura 3. El diagrama de flujo contiene la información de los acontecimientos que modelaron la Tierra como resultado de las fuerza operantes.

Tras el eón Hadeano (hace 3800 millones de años) la Tierra entró en una era de mayor tranquilidad. Se trata del eón Archeano, que llega hasta hace 2.5 Ga. Los acontecimientos consistieron en la aparición de las primeras tierras emergidas (más adelante, cratones) y posteriormente en la aparición de rocas y minerales, cuya mayor complejidad se alcanzó en los polímeros llamados silicatos.

Cuando en el enfriamiento del planeta se alcanzaron temperaturas inferiores a unos 100ºC, el vapor de agua que lo rodeaba se condensó formando mares y océanos.

A consecuencia de la actividad volcánica, emergieron los llamados “arcos de islas volcánicas” que más adelante formarían los cratones, antes o durante la aparición de las células prokariotas (hace unos 3.8 Ga).

A favor de las fuerzas actuantes (principalmente las gravitatorias) comenzaron los procesos de orogenia externa y eventualmente el transporte de materiales, debido a las diferencias de nivel existentes.

El agua formó estructuras análogas a las cuencas fluviales, siguiendo los pasos que se dan a continuación:

Movimiento inicial caótico?capilar(más organizado)?hilillos de agua?venas de agua ?arroyuelos?arroyos?afluentes?río principal (Figura 4).

Figura 4. En esta figura podemos apreciar el sistema utilizado en la evolución, tanto cósmica como planetaria y biológica: la formación de estructuras repetitivas.

Nótese la filosofía subyacente: se trata de un mismo motivo que se repite a escalas diferentes.

En la formación de los volcanes ocurrieron mecanismos análogos. Hay que tener presente que durante estos procesos la atmósfera no contenía oxígeno libre. Esto fue de gran transcendencia en muchos aspectos.

El oxigeno atmosférico libre apareció hace unos 2000 millones de años, que corresponde al eon Proterozoico, comprendido entre 2500 y 542 millones de años BP.

Durante un periodo tan dilatado de tiempo la atmósfera pasó de reductora a neutra-oxidante. Los mares y océanos eran reductores con contenidos importantes de iones ferrosos y uraninita.

A escalas mucho más pequeñas, próximas a las moleculares, pueden presentarse fenómenos locales, sobre todo en el transporte de fluidos, principalmente del agua, y gracias a su gran poder de disolución para los compuestos iónicos, derivado de su elevada constante dieléctrica. Estos últimos procesos se llaman de autoorganización geoquímica o sinergética [25].

Los anillos de Liessegang, el color dorado de algunas areniscas y las coloraciones en insectos y aves son manifestaciones actuales de esos mismos procesos locales de transporte y precipitación.

Una vez alcanzada una adecuada temperatura, que permitía la presencia del agua en sus tres estados, aparecieron las primeros microorganismos en mares someros: las células prokariotas [26-34]. Se ignoran los mecanismos abióticos que originaron el ADN. Uno de nosotros, ha desarrollado una teoría nuclear para explicar el origen de las proteínas.

Considerando los estromatolitos (Figura 5) como una arquitectura costera y comparándolos con el modelado precedente de la superficie se puede pensar que algo nuevo entró en escena.

Figura 5. Testigos de la actividad vital de los primeros organismos, como cianobacterias, los estromatolitos son un ejemplo de asociación biológica y geológica, que nos recordaría las placas dentarias y en general los filmes de bacterias.

La célula eukaryota apareció en la Tierra hace unos 2000 millones de años [35-38]. Entre la primitiva célula prokariota y la fauna ediacarense (Figura 6) (que al parecer exhibe un auténtico muestrario de fósiles) y, sobre todo, la del precàmbrico, transcurrió un enorme intervalo de tiempo, del cual no se conocen yacimientos fósiles.

Figura 6. Mostramos aquí un escenario de la fauna ediacarense que puede servirnos como ejemplo de las diversas formas que adoptaron los cuerpos vivientes en su evolución hasta formas y floras más recientes.

Como si se tratase del triunfo de la vida sobre la Tierra podemos observar estructuras tubulares, movimientos coordinados, ojos, etc., que nos hablan de neuronas y de sus conexiones.

Una estructura tan compleja como la de la célula eukariota explica que tardara tanto tiempo en encontrar su hábitat. Para preservar esta colonización parece lógico suponer que la célula eukariota adoptara la estrategia de la repetición del mecanismo que tanto tiempo había necesitado para desarrollarse.

Desde un punto de vista lógico parece más razonable admitir una estrategia de duplicación que cualquier otra, considerando que la misma es una característica singular de las moléculas del tipo DNA-RNA. Los enlaces de hidrógeno, son los únicos, quizás, que pudieron proporcionar los elementos de la cremallera (o piezas de un puzzle) que une las dos hebras de esos polímeros. Mucho antes de que se supiera ésto, se les había llamado puentes de hidrógeno.

A partir de esta base de seres vivos se formaron todos los demás de acuerdo con el darwinismo [5].

Las células deben absorber nutrientes de su medio ambiente y expulsar los desechos producidos. En un estado estacionario o cuasi-estacionario debe ocurrir que la velocidad de producción de desechos sea igual a la velocidad de su expulsión.

Como la producción de desechos es proporcional al volumen y su eliminación proporcional a la superficie, en el crecimiento de la célula puede ocurrir una acumulación de desechos y su envenenamiento [39].

Como hemos indicado, los organismos multicelulares aparecieron hace unos 580 millones de años con la fauna de Ediacara, anterior a la explosión cambriana (hace 542 millones de años) [40-42]. En estos organismos los aportes de nutrientes y del oxígeno dependen de la difusión a través de las superficies disponibles al efecto.

Este proceso es gobernado por la primera ley de Fick, según la cual la velocidad de transporte es proporcional a la superficie atravesada por el fluido y al gradiente de concentración.

Comparado con otros procesos de transporte, particularmente con el movimiento turbulento, la difusión es un proceso lento. Para aminorar esta lentitud los seres vivos construyeron grandes superficies con la disminución de su espesor: ciertos gusanos y algas; tubos huecos (coral); invaginación [6].

A pesar del aumento de la velocidad de absorción del oxígeno y de los nutrientes, debido a la mayor superficie de intercambio, el proceso de la difusión (desde el exterior), globalmente considerado, puede no ser suficiente, en muchos casos, para satisfacer las necesidades de una numerosa población de células (algunos miles de millones).

En esta situación, la solución, casi universal, consiste en adoptar la estrategia del transporte natural de materiales, como el caso de la cuenca de un río, debiendo tener en cuenta el hecho de que para las células debe hacerse mediante las conducciones más finas, lo que nos lleva a pensar en los capilares y en las leyes que gobiernan el movimiento de los líquidos a lo largo de los mismos.

Estas leyes se explican con el concurso de las llamadas fuerzas moleculares. El comportamiento del movimiento de los líquidos a través de capilares obedece a este tipo de fuerzas y en este caso se habla de la ley de Poisseuille.

Esta ley ha sido utilizada por algunos autores para modelizar la corriente sanguínea en mamíferos y en el cálculo del exponente de escala en el metabolismo basal [43].

En resumen, las diversas y sucesivas estrategias utilizadas fueron las siguientes:

Escisión celular, mitosis, creación de superficies (láminas y/o cintas extendidas, tubos huecos), superficies fractales, ramificación del transporte de materia-energía y ramificación para el transporte de información [44-46].

En la evolución de los seres vivos no hemos mencionado la temperatura de los diferentes sistemas que han ido apareciendo. Se sabe que la temperatura media ambiental (de unos pocos grados centígrados) era probablemente la correspondiente a los seres vivos, por razones de equilibrio. Hace unos 200 millones de años dicha temperatura experimentó un cambio brusco con la aparición de los mamíferos. Por ello, se produjo un aumento notable de la velocidad de especiación, como si se tratara de una nueva explosión precámbrica (que podemos caracterizar por el crecimiento del cerebro y cerebelo con relación a la masa corporal). Aproximadamente hace unos 2.5 millones de años apareció nuestra especie.

El crecimiento

El crecimiento va acompañado de una ocupación del espacio disponible y, por lo dicho anteriormente, esta ocupación debe facilitar los intercambios materiales y energéticos [47]. En los animales, como es el caso de los embriones en el huevo, el espacio disponible para el crecimiento se halla lleno con el material de reserva, el cual va siendo sustituido por él [48-52]. Si el espacio disponible se llenara de materia, los intercambios estarían limitados debido a que la difusión a través de la materia condensada es un proceso lento (es la difusión molecular). Esta es la explicación de que el vegetal desarrolle una estructura fractal que no es compacta, pero que posee la suficiente frondosidad que facilita la difusión turbulenta con la finalidad de que los nutrientes alcancen fácilmente la superficie de las hojas [53-55].

La imagen de la fractalidad vegetal sería ésta: de un tronco salen ramas y de éstas, otras ramas y así sucesivamente hasta la yema terminal. El éxito de los vegetales quizá sea debido al hecho de la disponibilidad del espacio aéreo exterior y también, aunque en menor grado, la del espacio terráqueo, en el seno del cual las raíces constituyen también una estructura fractal, sí bien, no tan claramente como en el caso de las hojas.

Para los animales el espacio disponible es el del huevo y/o útero, por lo que el crecimiento en este caso está fuertemente constreñido. Mientras el tamaño del embrión es pequeño en relación con el de su contenedor, nada se opone al crecimiento, pero al cabo de un cierto tiempo se puede advertir la precariedad del espacio disponible, que coincide grosso modo con la aparición de las somitas. Cuando el embrión ocupa casi todo el espacio, el crecimiento tiene lugar “hacia dentro” originándose, por las mismas causas señaladas para los vegetales, estructuras fractales, la más fácil de visualizar es la de los pulmones, que podría considerarse como un “árbol interior” (Figura 7). El sistema circulatorio es otra estructura fractal, fácilmente localizable [56-58]. El crecimiento fractal es coherente con el darwinismo puesto que su estructura repetitiva implica una programación genética comparativamente muy simple, un aspecto que hace notar Dawking en su libro “ El Río del Edén” [59].

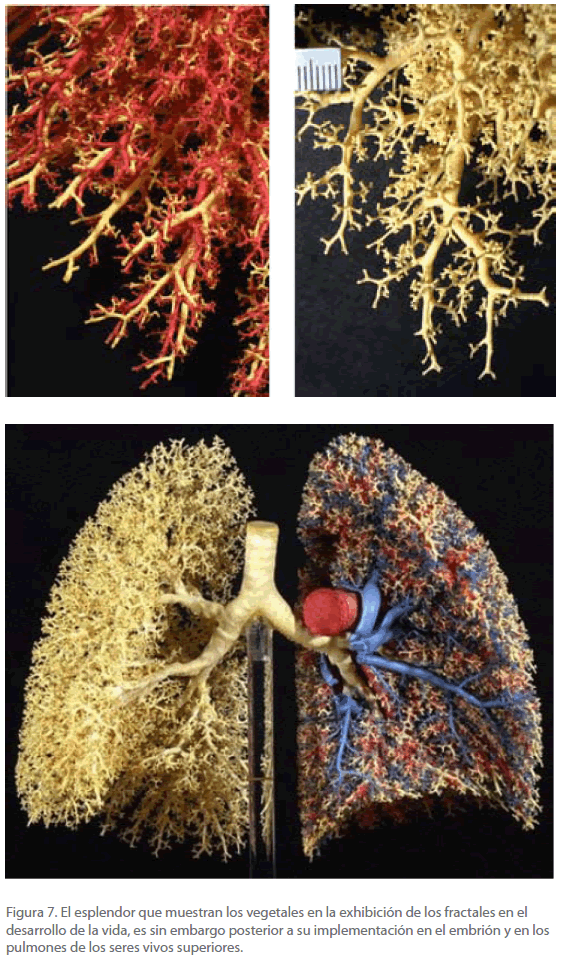
Figura 7. El esplendor que muestran los vegetales en la exhibición de los fractales en el desarrollo de la vida, es sin embargo posterior a su implementación en el embrión y en los pulmones de los seres vivos superiores.

Si conociéramos la relación entre el tiempo t y la masa m, es decir, m versus t, dispondríamos de una valiosa información acerca de la historia del proceso, pudiéndose deducir cómo han ido variando ciertas características del mismo, tales como la velocidad. Aunque no se mencione explícitamente, se supone que estos procesos transcurren a temperatura prácticamente constante. Necesitamos previamente disponer de los conceptos necesarios para abordar este estudio. El metabolismo nos proporciona una valiosa ayuda al respecto [60-62].

En efecto, pues como es sabido, se trata de la energía emitida por unidad de tiempo (B Julios/seg) y que se representa en la forma de una ecuación alométrica (B=B0 ¥ mb) en la que la masa del animal está elevada a la potencia b, cuyo valor es alrededor de 0.7.

Pero ¿cuál es el significado y alcance de la potencia b?. Para resolver esta cuestión hay que aplicar el principio de conservación de la energía para diversos tipos de animales, por ejemplo entre los mamíferos. Dicho principio significa que cualquiera que sea el animal, la energía canjeada durante su tiempo medio de vida debe ser el mismo para la unidad de masa, esto es, el gramo. Aceptando que ese tiempo de vida venga dado por una ecuación alométrica (t=t0 ¥ mc) [63-68], resulta que se verifica que b+c~1. La hipótesis precedente viene apoyada por las medidas experimentales.

Al ser c un valor del orden de 0.3, encontramos una relación entre el tiempo de gestación y la masa del feto a término. Y más general, si conocemos b y c, podemos considerar la ecuación anterior como si la masa fuese una función del tiempo transcurrido. Vamos a estudiar experimentalmente este proceso de desarrollo.

Los datos proporcionados por la literatura se han ajustado mediante el MATLAB [69,70]. La bondad del ajuste se puede expresar de distintas maneras, de acuerdo con la estadística. La más sencilla e intuitiva a nuestro juicio la proporciona r2, coeficiente de determinación, en el sentido de que dicho valor representa el porcentaje de la totalidad de los valores de m que caen dentro de la recta; el resto de valores, o sea (1 – r2)% caerán a cada lado de la misma, y son los llamados valores residuales. La recta es logaritmo de m versus logaritmo de t.

En la figura 8 se incluyen los valores del coeficiente de correlación y del exponente c, para las aves que se citan.

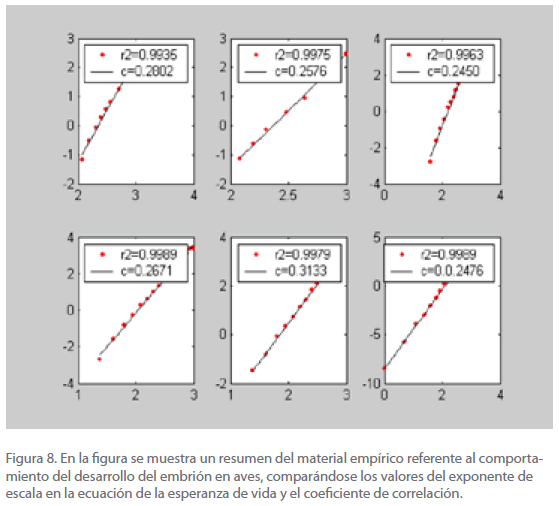
Figura 8. En la figura se muestra un resumen del material empírico referente al comportamiento del desarrollo del embrión en aves, comparándose los valores del exponente de escala en la ecuación de la esperanza de vida y el coeficiente de correlación.

Resumiendo, diríamos que en los casos considerados la función de la forma explicada anteriormente es la más idónea, por no decir la única. Lo más notable del estudio anterior es la aparente ausencia del periodo embrionario, o su difícil seguimiento, desde el tiempo cero en adelante.

Embrion-feto humano

Los datos proporcionados por la literatura se refieren a tamaños (en mm) del embrión-feto en función del tiempo transcurrido (en días). Al término de unos dos meses, los valores del individuo se dan en gramos.

Con la ayuda del Matlab hemos ensayado ajustes a ecuaciones con el menor número de parámetros. Las mejores ecuaciones fueron la exponencial y la potencial, siendo esta última la que mejor se adapta a los valores experimentales y a los extrapolados. La ecuación es d=3.106*!0-4 t2.747 mm (t en días). La misma serie de valores muestra que 470 mm corresponden a 3100 gramos. Tomando para la masa de la célula media el valor 6*10-10 gr, se obtiene:

N=1.1*1010 *d células, y D=1.44*log(N) divisiones.

El hábito de la ecuación anterior (D versus t) indica un comportamiento inicial caracterizado por un ascenso prácticamente instantáneo, que con el transcurso del tiempo va disminuyendo, como indica claramente la presencia de una curvatura. Consideremos primeramente lo que sucede hasta la aparición de la curvatura. Este comportamiento es la traducción de los sucesivos procesos que tienen lugar en los comienzos del desarrollo embrionario, el más importante de los cuales consiste en un apelotonamiento compacto de células que recordaría a una esfera o balón de football [71-73]. Para una sola célula, la relación superficie/ volumen es enorme, de manera que inicialmente no existen problemas de intercambio. Al dividirse la célula y apelotonarse (Figura 9) crece la superficie, pero no tanto como si las células no sufrieran este proceso, por lo que a medida que el tiempo aumenta, la relación entre la superficie de intercambio y el volumen disminuye, poniendo en peligro la subsistencia debido a la acumulación de residuos.

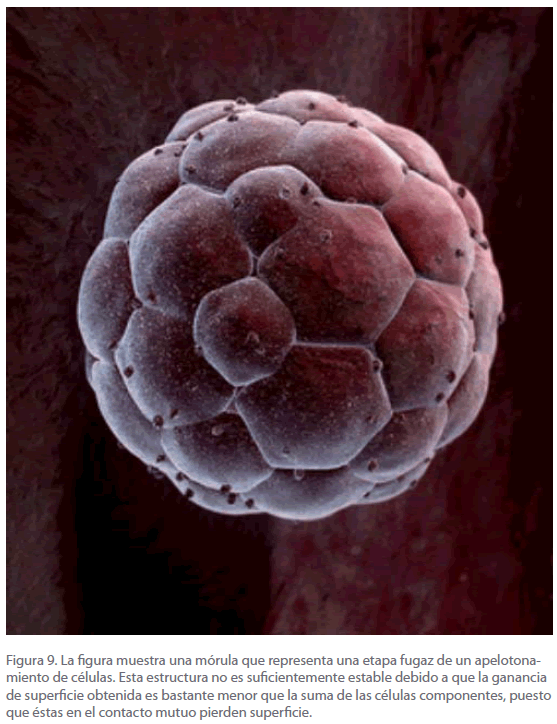
Figura 9. La figura muestra una mórula que representa una etapa fugaz de un apelotonamiento de células. Esta estructura no es suficientemente estable debido a que la ganancia de superficie obtenida es bastante menor que la suma de las células componentes, puesto que éstas en el contacto mutuo pierden superficie.

El problema se resuelve gracias a la invaginación, proceso que consiste en la transformación del apelotonamiento esférico en una estructura celular con doble pared, con lo cual la superficie aumenta a valores que facilitan la subsistencia del sistema, que pasa del último apelotonamiento, llamado mórula, a los siguientes. Mencionemos aquí que los organismos que podríamos llamar morulares, no existen o son muy raros. La ralentización que se produce a continuación se debe a los procesos de emigración de las células madre.

En el desarrollo embrionario las variables utilizadas son masas y/o tamaños y tiempos transcurridos, cuya relación es la de la expresión anterior. Si en lugar de utilizar estas variables hacemos uso de las reducidas, que se obtienen dividiendo cada una de ellas entre el valor correspondiente al término final, ocurre que para un mismo o aproximado valor de c, obtenemos la misma ecuación, o dicho de otra manera, “para los mismos valores del tiempo reducido, las características del embrión-feto son aproximadamente idénticas”. Aplicadas al embrión y al feto proporcionan resultados diferentes, porque los embriones se parecen mucho más entre sí que los fetos entre ellos, o dicho en otros términos, las características de unos y otros para los mismos tiempos reducidos siendo las mismas, son menos evidentes en el embrión que en el feto, pues el embrión de un elefante no exhibe pico y el ave no exhibe trompa.

Todo lo anterior se puede resumir en el sentido de que, para el caso del embrión humano y en general para todos los mamíferos, el fenómeno de crecimiento desde la fecundación al nacimiento consta esencialmente de dos etapas, la embrionaria y la fetal. El hecho de que el mamífero más conspicuo sea el Homo sapiens, induce a pensar que el comportamiento de los mamíferos sea análogo, lo cual nos lleva a considerar que el tiempo reducido correspondiente a todos ellos sea el mismo, o en otras palabras, que todos los embriones se parezcan entre sí (Figura 10), y por lo tanto, exhiban formas análogas, pero que los fetos correspondientes sean completamente diferentes.

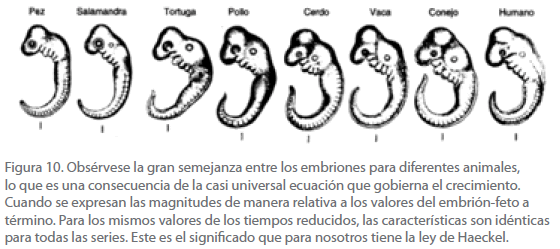
Figura 10. Obsérvese la gran semejanza entre los embriones para diferentes animales, lo que es una consecuencia de la casi universal ecuación que gobierna el crecimiento. Cuando se expresan las magnitudes de manera relativa a los valores del embrión-feto a término. Para los mismos valores de los tiempos reducidos, las características son idénticas para todas las series. Este es el significado que para nosotros tiene la ley de Haeckel.

Macroscópicamente consideradas las diferencias entre los fetos contrastan con la semejanza entre los embriones. Lo extraordinario de este comportamiento se explica por la emigración de las llamadas células madre, es decir, que una vez terminada la fase de embrión, haya células que tomen caminos diferentes para formar tejidos diferentes: un pico en las aves, una trompa en el elefante y un boca en el homo-sapiens. ¿Quién dicta a las células indiferencias del embrión maduro las órdenes para que “sepan” qué camino tomar de tal manera que no haya elefantes con pico o ratones con trompa? La respuesta es evolución y expresión genética [74-76].

Ley de Haeckel

Comparando un tanto arbitrariamente las formas embrionarias de algunas especies (Figura 11), Haeckel enunció que “La ontogenia recapitula la filogenia”, entendiendo que la primera se refiere al crecimiento y desarrollo de un individuo y la segunda a la historia de la evolución de la correspondiente especie. En otras palabras, cada sucesivo estadio en el desarrollo actual de un embrión-feto, corresponde a un antepasado adulto de la historia de la especie considerada. Refiriéndonos, por ejemplo, a la especie homo-sapiens, y considerando que en la evolución de las especies ha sido precedida por los peces, anfibios y reptiles, las diferentes formas que exhibe el desarrollo embrionario corresponden, según Haeckel, a las formas adultas de las especies citadas y en el mismo orden [77].

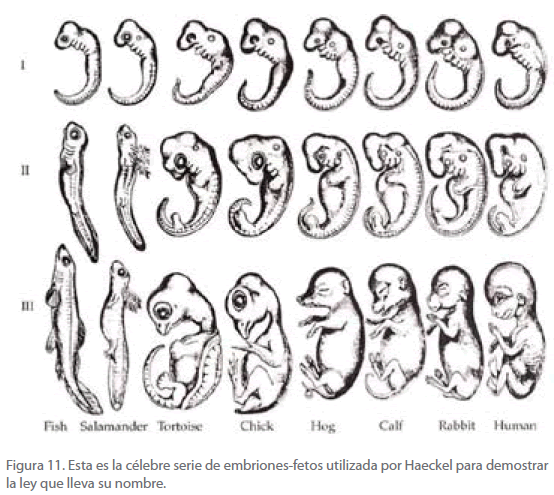
Figura 11. Esta es la célebre serie de embriones-fetos utilizada por Haeckel para demostrar la ley que lleva su nombre.

A pesar de que la teoría mencionada ha sido desacreditada por la moderna Biología, su influencia ha sido muy notable, habiéndose incluso ampliado a otros campos. Por nuestra parte, creemos que los conceptos introducidos acerca de la sincronía y diacronía tienen mucho en común, no solo en el lenguaje, sino en otros campos, como es por ejemplo el de la tabla periódica [78] en la cual la estructura electrónica de un elemento (sincronismo) recapitula (diacronismo) la serie de todas las estructuras anteriores. Nuestra posición al respecto es que la ley de Haeckel no existe.

Estos deben ser, en todo caso, algunos conceptos importantes relacionados con los intentos de Haeckel para extrapolar la gran semejanza entre los embriones que estudió.

Admitiendo la actual doctrina acerca del universo y la universalidad de las fuerzas operantes (magnitudes primarias), se introduce un nuevo modo de descripción coherente para todos los objetos formados en el curso de su evolución y en particular para los correspondientes a nuestro entorno más próximo. Esta metodología globalizadora e integradora, contribuye a clarificar conocimientos muy importantes acerca del universo en general y de la Tierra, como el único asentamiento más próximo del fenómeno vida, en particular.

858

References

1.  Thompson DW. Sobre el crecimiento y la forma. Madrid: Hermann Blume Ediciones, 1980.
2.  Prigognie I. El fin de las certidumbres. Madrid: Editorial Taurus Ciencias, 1997.
3.  Narlikar J. The structure of the Universe. Oxford: Oxford University Press, 1997.
4.  Wolpert L. The Triumph of the Embryo. Oxford: Oxford University Press, 1998.
5.  Sadler TW. Langman Embriología médica. Buenos Aires: Médica Panamericana, 2004.
6.  Gilbert SF. Biología del desarrollo. Buenos Aires: Médica Panamericana, 2004.
7.  Davies P. El universo accidental. Barcelona: Biblioteca Científica Salvat, 1987.
8.  Garzón L. Historia de la materia, del Big-Bang al origen de la vida. Oviedo: Ediciones Nobel, 1994.
9.  Garzón L. Los orígenes de la vida. Mundo Científico 2001;219,12-19
10.  Hoyle F. El Universo: galaxias, núcleos y quasars. Madrid: Alianza editorial, 1967.
11.  Hoyle F. El Universo inteligente. Barcelona: Ediciones Grijalbo, 1984.
12.  Audouze J and Israel G. The Cambridge atlas of astronomy. Cambridge: Cambridge University Press, 1985.
13.  Koolman J and RöhmK-H. Bioquímica. Buenos Aires: Médica Panamericana 2004.
14.  Maillet M. Biología celular. París: Editorial Masson, 2000; p.127-166.
15.  Oberai A, Yungok I, Sanguk K and Bowie JU. A limited universe of membrane protein families and folds. Protein Sci 2006;15:1723-1734.
16.  Choi and Kim S-H. Evolution of protein srtructura classes and protein sequence families. PNAS 2006;38:14056-14061.
17. Dose K, Bieger-Dose A, Kerz O and Gill M. DNA-strand breaks limit survival in extreme dryness. Origins of Life and Evol Biosphere 21:177-178.
18. Gimeno MJ et al. Autoorganización Geoquímica. Estudios geol 1989;45:315- 324.
19. Garzón L. Biological life and temperature: a semiempirical approach. Origins of life and evolution of biosphere 2003;36:10-16.
20. Garzón L. El origen de la vida. Un nuevo escenario. Oviedo: Servicio de publicaciones de la Universidad, 1996.
21. McKee S and Gould GW. A simple matematical model of the termal death of microorganisms. Bull Math Biol 1988;50(5):493-501.
22. Cossins AR and Bowler K. Temperature biology of animal. London: Chapman and Hall, 1987.
23. Cairns-Smith AG. Siete pistas sobre el origen de la vida. Madrid: Alianza Ediciones del Prado, 1994.
24. Margulis, L. El origen de la célula. Barcelona: Editorial Reverté, 1988.
25. Clark BC et al. Survival of life on asteroids, comets and other small bodies. Origins of Life and Evol of the Biosphere 1999;29:521-545.
26. Kurland CG, Collins LJ, Penny D. Genomics and the irreductible nature of eukaryote cells. Science 2006;312:1011-1014.
27. Margulis L and Sagan D. Microcosmos. Barcelona: Tusquets Editores, 1995.
28. Margulis L and Sagan D. ¿Qué es la vida? Barcelona: Tusquets Editores, 1996.
29. Nicholson WL, Munakata N, Horneck G, Melosh NJ and Setlow T. Resistance of Bacillus endospores to extreme terrestrial and extraterrestrial environments. Microbiology an molecular biology reviews 2000;64(3)548.
30. Skiner GE, Larking JW and Rhodehamel EJ. Mathematical modelling of microbial growth: A review. J Food Safety 14,175-217.
31. Shen B, Dong L, Xiao S, Kowalewski M. The Avalon Explosion: Evolution of Ediacara morphospace. Science 2008;319:81-84.
32. West GB, Woodruff VH and Brown JH. Allometric scaling of metabolic rate from molecules and mitochondria to cells and mammals. Proc Natl Acad Sci U.S.A. 2002; 99:2473-2478.
33. Altman PL and Ditter DS. Biology data book. Bethseda MD: Fed Amer Exp Biol Vol 1,1972&Vol 3, 1974.
34. Azbel MY. Universal biological scaling and mortality. Proc Natl Acad Sci USA 1994;91:12453-12457.
35. Brack A, Hornech G and Wynn-Willians D. Exo/Astrobiology in Europe. Origins of Life and Evol of Biosphere 2001;31:459-480.
36. Deeming DCh and Ferguson WJ, MWJ editores. Eggs incubation: its effects on embryonic development in birds and reptiles. Australia: Cambridge University Press, 1995.
37. Starck JM and Ricklefs RE Editores. Avian growth and development. Oxford: Oxford University Press, 1998.
38. Harrison C. Guía de campo de los nidos, huevos y polluelos de las aves de España y de Europa. Barcelona: Ediciones Omega, 1991.
39. Slack JMW. From egg to embryo. Regional specification in early development. U K: Cambridge University Press, 1997.
40. Mandelbrot B B. The fractal Geometry of Nature. New York: W. H. Freeman, 1983.
41. Mandelbrot B B. Los objetos fractales. Barcelona: Tusqets editores, 2006.
42. Mandelbrot B B. How long is the coast of Britain? Statistical Self-similarity and fractional dimension. Science 1967;156(3775):636-8.
43. Goldberger AL, Amaral LA, Hausdorff JM, Ivanov PC, Peng CK, Stanley HE. Fractal dynamics in physiology; alterations with disease and aging. Proc Natl Acad Sci 2002;99(Suppl 1):2466-2467.
44. Kalliokoski K, Kuusela A, Laaksonen S, Knuuti J and Nuutila P. Muscle fractal vascular branching pattern and microvascular perfusion heterogeneity in endurancetrained and un trained men. J Physiol 2003;546.2:529-535.
45. Dodds AJ, Rothman DH and Weitz JS. Re-examination of the _ law of Metabolism. JTheor Biol 2001;209:9-27.
46. White and Seymour. Mammalian basal metabolic rate is proportional to body mass2/3. PNAS 2003;100:4046-4049.
47. Smidt-Nielsen K. Why is animal size so important?. Cambridge: Cambridge University Press, 1984.
48. White CR and Seymour RS. Allometric scaling of mammalian metabolism. Journal of experimental Biology 2005;208:1611-1619.
49. Enquist BJ, Brown JH and West. Allometric scaling of plant energetic and population density. Nature 1998;395:163-165.
50. Enquist BJ, West GB, Charnov EI and Brown JH. Allometric scalling and life-history variation in vascular plants. Nature 1999;401:907-91.
51. Dickson BG. Growth, debate, and progress in biological allometry. For Sci 2001;47:201-228.
52. Vázquez L, Dobado A and Sánchez JP, editores. Alometrías en Biología: una perspectiva cosmológica. XXIX Reunión Bienal de la RSEF; Sevilla 2003.
53. West GB, Brown JH and Enquist BJ. The fourth dimension of life: fractal geometry and allometric scaling of organisms. Science 1999 a;284:1677-1679.
54. Pérez C. Matemática informatizada con MATLAB. Madrid: RA-MA Editorial, 1996.
55. Richardson MK, Allen PS, Wright MG, Raynaud A and Hanken J. Somite number and vertebrate evolution. Development 1998;125:151-160.
56. Wolpert L, Beddington R, Jessell T, Lawrence P, Meyerowitz E, Smith J. Principles of Development. Barcelona: Oxford University Press, 2002.
57. Keller JP, Schmidt DA, Wittbrodt J and Stelezer HK. Reconstruction of zebrafish early embrionic development by scanned light sheet microscopy. Science 2008; 322:1065-1069.
58. Richardson MK and Verbeek FJ. New directions in embryology and the nature of developmental characters. Animal Biology 2003;53:303-311.
59. Banavar JR, Damuth J, Maritna A, Rinaldo A. Ontogenic growth: modelling universality and scaling. Nature 2002;420:626.
60. Garzón L. De Mendeleiev a los superelementos. Oviedo: Servicio de publicaciones de la Universidad, 1996.