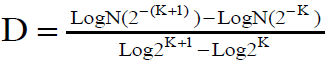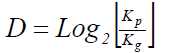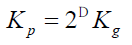Archivos de Medicina

Keywords

Cardiovascular disease; Dynamic systems; Diagnosis; Holter

Introducción

La teoría de los sistemas dinámicos analiza el estado y la evolución de los sistemas, mediante el cambio de sus variables en el tiempo [1]. Usualmente, se representa la dinámica en el llamado espacio de fases, donde es posible originar atractores que describen la trayectoria y tendencia del sistema. Los atractores caóticos que representan dinámicas impredecibles [2], se caracterizan por sus formas irregulares. Se distinguen dos tipos de caos: el determinista y el estocástico; el primero es caracterizado su no linealidad y por la imposibilidad de su predicción a largo plazo o el reconocimiento de propiedades estadísticas de las trayectorias [3]. El segundo es caracterizado por ser no determinista [4] y por estar asociado a factores predecibles como a elementos aleatorios, además de una duración nula de la memoria estadística [5], impidiendo establecer predicciones.

Durante el siglo XX, los atractores caóticos y otras formas que presentaban estructura irregular fueron denominadas fractales. Las formas geométricas clásicas son regulares y tienen dimensiones enteras (1, 2, y 3, para la línea, la superficie y el volumen, respectivamente); Mientras que los fractales son muy irregulares, tienen dimensiones fraccionarias y presentan autosemejanza, propiedad que utilizó Mandelbrot [6] para mostrar lo inapropiado de medir con geometría euclidiana los objetos irregulares. Una amplia variedad de formas naturales comparten esta propiedad de autosemejanza, incluyendo formaciones de coral, costas y cordilleras irregulares. Un número de estructuras cardiopulmonares también tienen una apariencia fractal [7-10]. Ejemplos de anatomías auto-similares incluyen las redes arteriales y venosas, la ramificación de ciertos haces musculares, el árbol traqueobronquial, entre otros.

Las enfermedades cardiovasculares lideran las causas de mortalidad en Europa, causando 4 millones de muertes al año [11], con porcentajes de mortalidad para mujeres del 51%, y para hombres del 42%, cifras elevadas si las comparamos con las muertes ocasionadas por todos los tipos de cáncer en Europa, 19% y 23%, respectivamente. En Norteamérica el panorama no es más alentador [12]; las tasas de mortalidad por enfermedad coronaria han aumentado en Estados Unidos y en muchos países europeos [13]. En el resto del mundo, las estadísticas confirman que estas enfermedades son la principal causa de muerte; de acuerdo con la Organización Mundial de la Salud [14] en el 2012 murieron cerca de 17,5 millones de personas.

El Holter ha sido considerado como una de las más importantes herramientas de ayuda diagnóstica para identificar alteraciones significativas del ritmo cardíaco transitorias o de presentación súbita [15]. El análisis del intervalo RR ha mostrado utilidad clínica en la detección de alteraciones del sistema cardíaco [16-18].

Las teorías físicas y matemáticas como la teoría de los sistemas dinámicos [1], la ley del caos [19] y la geometría fractal [20] han sido aplicadas a la fisiología cardíaca, evidenciando su comportamiento irregular [21]. Desde los sistemas dinámicos y los sistemas no lineales Goldberger y Cols. realizaron una nueva interpretación de la concepción de normalidad-enfermedad, caracterizando la enfermedad por comportamientos muy aleatorios o muy regulares y periódicos, y la normalidad como un estado intermedio entre los dos comportamientos descritos [22]. Desde ésta perspectiva, se han propuesto nuevos índices a partir de análisis fractales de la variabilidad de la frecuencia cardíaca [23], no obstante aún se requieren estudios para corroborar su aplicabilidad clínica.

Continuando con esta línea de investigación, Rodríguez y Cols. desarrollaron una ley exponencial caótica de la dinámica cardíaca a partir de la cual se establecieron diferenciaciones cuantitativas entre dinámicas normales, patológicas agudas y aquellas que se encuentran en evolución hacia la enfermedad [24-26]. El propósito de este trabajo es hacer una aplicación de esta metodología, inicialmente empleada en el análisis del sistema cardíaco n 21 horas, en el contexto de una reducción a 16 horas, realizando una contrastación entre el diagnóstico físicomatemático y el Gold Standard.

Materiales y Método

Mapa de retardo: Tipo de atractor específico, que se construye en un espacio cartesiano a partir de los pares ordenados de valores correspondientes a una variable dinámica del sistema. Estos valores son consecutivos en el tiempo. Para este caso la variable es la frecuencia cardíaca.

Ecuación 1: Dimensión fractal de box-counting (D)

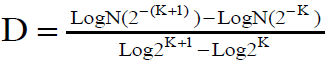
N corresponde al número de cuadros ocupado por el objeto en la cuadricula de grado de partición K.

Ecuación 2: Ecuación de Box-Counting simplificada

Para las medidas realizadas en este trabajo, se usaron dos cuadrículas, denominadas Kp y Kg que tienen una proporción de ½ en los lados de los cuadros; de esta forma, la ecuación de la dimensión fractal se puede simplificar:

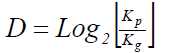
Kp es el número de cuadros ocupados por la cuadrícula más pequeña y Kg los correspondientes a la cuadricula grande.

Ecuación 3: Ley exponencial de la dinámica caótica cardíaca

Anteriormente se dedujo una ley general para la dinámica cardíaca caótica [19], con la que puede ser cuantificado cualquier atractor. La expresión matemática de esta ley es:

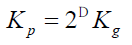
Población

Fueron tomados 80 registros electrocardiográficos continuos y Holters, pertenecientes a sujetos mayores de 21 años, de mínimo 21 horas, de los cuales 10 correspondieron a casos diagnosticados por un cardiólogo experto como dentro de límites normales y 70 casos correspondieron a casos diagnosticados con diferentes tipos de patología. Los registros fueron tomados de bases de datos previas del grupo Insight.

Procedimiento

Inicialmente se enmascararon los diagnósticos clínicos. Para generar los atractores caóticos de cada dinámica, fue necesario tomar de cada registro electrocardiográfico, los valores máximos y mínimos de las frecuencias cardíacas y el número total de latidos por hora. Esta información fue tomada para generar una secuencia pseudoaleatoria de frecuencias cardíacas mediante un algoritmo equiprobable, empleando un Software previamente desarrollado [24-26]. Con base en dicha secuencia, fueron graficadas parejas ordenadas de frecuencias cardíacas, dando lugar al mapa de retardo (ver definiciones). Luego, se procedió a cuantificar los espacios ocupados, Kp y Kg por cada atractor, superponiendo dos rejillas, cuya proporción de longitud entre los lados de los cuadros es de 1:2, y se calculó la dimensión fractal por medio del método de Box-counting (Ecuación 2).

Se estableció el diagnóstico físico y matemático de cada uno de los registros electrocardiográficos, empleando para ello la Ecuación 3 y tomando como base los parámetros numéricos de la metodología previamente desarrollada [24]; de esta forma, una dinámica cardíaca con características físico-matemáticas de enfermedad aguda se estableció cuando se hallaron espacios de ocupación Kp inferiores a 73, para valores mayores a 200 se estableció un diagnóstico físico-matemático de normalidad, mientras que un estado de evolución hacia la enfermedad aguda se caracterizó por espacios de ocupación entre 73 y 200. Este procedimiento fue realizado, tanto para 21 como para 16 horas. Luego, se evaluó la concordancia entre los diagnósticos matemáticos en 21 y 16 horas.

Análisis estadístico

Los resultados diagnósticos de los registros electrocardiográficos determinados por el cardiólogo experto de acuerdo con los parámetros convencionales, fueron tomados como Gold Standard y desenmascarados para efectos del análisis estadístico. Una vez confirmada la concordancia entre el diagnóstico matemático establecido en 21 y 16 horas, se compararon los diagnósticos convencionales con los diagnósticos establecidos con la reducción del tiempo de evaluación. Se calculó la sensibilidad y la especificidad, a partir de una tabla de contingencia de 2*2, teniendo en cuenta los verdaderos positivos, los verdaderos negativos, los falsos positivos y falsos negativos. Se evaluó el nivel de concordancia entre el diagnóstico matemático y el convencional mediante el coeficiente Kappa.

Aspectos éticos

Tanto los principios éticos de la Declaración de Helsinki de la Asociación Médica Mundial como los requisitos de la Resolución 8430 de 1993 del Ministerio de Salud Colombiano enmarcan el desarrollo de la presente investigación, que es categorizada como de mínimo riesgo, pues se realizan cálculos físicos y matemáticos sobre reportes de exámenes que han sido prescritos previamente según protocolos médicos convencionales. El anonimato e integridad de los participantes fue protegido.

Resultados

Todos los atractores correspondientes a las dinámicas cardíacas presentaron valores de dimensiones fractales entre 0,8101 y 1,9372 para 21 horas, mientras que para 16 horas estuvieron entre 0,8101 y 1,9883. Respecto a los espacios ocupados en la rejilla Kp, se encontraron valores entre 47 y 347 para 21 horas, y entre 46 y 350 para 16 horas (Tabla 1).

Holter No.	Indicaciones	21 horas			16 horas
		Kp	Kg	DF	Kp	Kg	DF
1	Normal	328	123	14,150	330	121	14,475
2	Bloqueo cardíaco tercer grado	48	13	18,840	52	14	18,931
3	Normal	347	93	18,990	350	94	18,966
4	FA, mareo	186	75	13,103	188	75	13,258
5	Molestia torácica	120	33	18,625	123	31	19,883
6	opresión torácica	186	74	13,297	191	76	13,295
7	CIA, mareo	188	50	19,107	184	52	18,231
8	Normal	254	73	17,989	257	74	17,962
9	Normal	322	86	19,047	324	88	18,804
10	Arrirmia, palpitaciones, correlacionados con taquicardia sinusal. Ectopia auricular frecuente y aislada.	182	68	14,203	178	66	14,313
11	HTA	74	35	10,802	79	33	12,594
12	Normal	294	81	18,598	295	81	18,647
13	Normal	321	117	14,561	323	115	14,899
14	Insuficiencia cardíaca, CIA	47	16	15,546	46	15	16,167
15	Normal	294	107	14,582	295	107	14,631
16	Normal	263	150	0,8101	263	150	0,8101
17	Taquicardia, ligera tendencia a taquicardia sinusal	180	47	19,373	176	47	19,048
18	Normal	248	117	10,838	250	117	10,954
19	Secundum CIA	133	61	11,245	135	63	10,995
20	Normal	288	77	19,031	292	79	18,860
21	Desmayo (síncope)	187	102	0,8745	182	103	0,8213

Kp y Kg: Número de cuadros ocupados por el atractor en las rejillas de cuadros pequeños y grandes, respectivamente; DF mayúsculas: Dimensión Fractal mayúsculas.

Tabla 1: Medidas y diagnostico convencional de algunos de los casos estudiados.

Las dinámicas cardíacas que corresponden a enfermedad aguda exhibieron valores de ocupación espacial inferiores o iguales a 73 con la rejilla Kp, tanto para 21 horas como para 16 horas; mientras que valores mayores a 200, se encontraron para los registros dentro de límites normales. Se puede observar las diferencias entre el espacio de ocupación de un atractor de una dinámica normal y uno de una dinámica aguda (Figura 1).

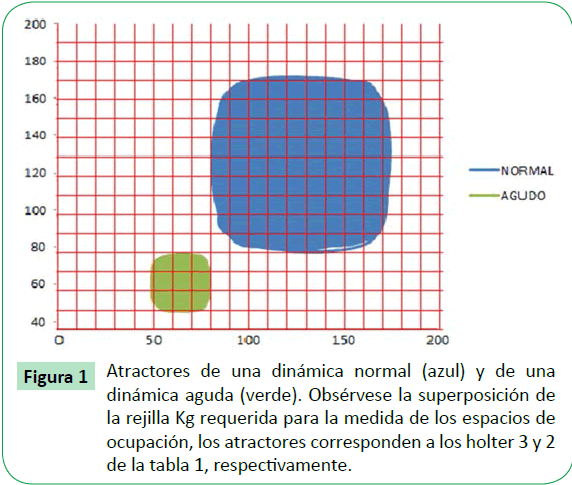
Figure 1:Atractores de una dinámica normal (azul) y de una dinámica aguda (verde). Obsérvese la superposición de la rejilla Kg requerida para la medida de los espacios de ocupación, los atractores corresponden a los holter 3 y 2 de la tabla 1, respectivamente.

Al realizar el análisis estadístico, los valores de sensibilidad y especificidad fueron del 100%, y el coeficiente Kappa fue igual a 1, indicando la máxima concordancia diagnóstica entre la reducción a 16 horas de la ley y el Gold estándar.

Discusión

Este es el primer trabajo en el que se aplica una ley matemática exponencial de la dinámica cardíaca [24] a 80 registros electrocardiográficos en el marco de una reducción del tiempo de evaluación a 16 horas, mostrando la capacidad de la metodología de diferenciar y diagnosticar matemáticamente casos de enfermedad aguda, casos dentro de límites normales y en evolución, permitiendo cuantificar las dinámicas que van evolucionando hacia enfermedad aguda, constituyéndose así en una metodología preventiva, de ayuda diagnóstica pues puede mostrar anticipadamente la evaluación de la dinámica a partir de la disminución de los espacios de ocupación del atractor en el espacio de fases. Además la aplicación de la reducción de la metodología a 16 horas permite una evaluación que optimice tiempo y recurso.

En la fisiología clásica las nociones de normalidad y enfermedad están basadas en el comportamiento regular y periódico de las dinámicas [27], el análisis de la dinámica cardíaca desde teorías físicas y matemáticas de la dinámica cardíaca ha permititdo el desarrollo de nuevas concepciones, Goldberger y cols. analizaron dicha dinámica a partir de los sistemas dinámicos, evidenciando que una dinámica enferma estará asociada a un comportamiento regular y periódico o muy aleatorio y complejo, mientras que el comportamiento de una dinámica normal se encuentra entre estos dos extremos.

El desarrollo de la ley exponencial de la dinámica caótica cardíaca evidencia que es posible establecer parámetros cuantitativos de seguimiento de los pacientes, que sean más objetivos y reproducibles y de ayuda en la toma de decisiones clínicas. Por su carácter matemático la ley no establece correlaciones causales, como los métodos generalmente estudiados en la fisiología clásica, los cuales están basados en métodos estadísticos lineales que consideran la normalidad como el ideal de regularidad, estabilidad y periodicidad.

La reducción a 16 horas de la ley aplicada en este trabajo ha evidenciado que la dinámica cardíaca presenta una autoorganización [24] que permite establecer un diagnóstico matemático para cada dinámica en menor tiempo y haciendo abstracción de relaciones causa - efecto así como de variables epidemiológicas y estadísticas. La metodología ha mostrado su aplicabilidad clínica [25,26], siendo de utilidad para el estudio predictivo de la dinámica cardíaca, asi como para el diseño futuro de dispositivos para el seguimiento y monitoreo remoto de la dinámica cardíaca tales como cardiodesfibriladores implantables y marcapasos.

El análisis acausal establecido por las formas de razonamiento de la física teórica moderna como la teoría del caos [1,19,28], la mecánica cuántica [29] y la mecánica estadística [30,31] permiten comprender los fenómenos de manera más simple. Esta metodologia está basada en esta forma de razonamiento, permitiendo hacer la simplificación lograda que implica la reducción del tiempo a 16 horas. Este tipo de perspectiva de investigación ha sido aplicado en diferentes áreas como la morfometría celular [32,33] y arterial [34]; la cardiología [35- 39]; la inmunología [40]; la hematología [41]. En infectología se desarrollaron dos metodologías altamente predictivas de la población de linfocitos T CD4 [42,43] a partir de la información del cuadro hemático y en epidemiología, se logró predecir en 820 municipios de Colombia brotes de malaria [44] y dengue [45]. También se han logrado establecer predicciones matemáticas de mortalidad [46] en la Unidad de Cuidados Intensivos (UCI).

Conclusión

Se logra una reducción para la aplicación de esta metodología al estudió de la dinámica cardíaca caótica a 80 registros Holter en 16 horas de la ley caótica exponencial de la dinámica cardíaca, evidencia su utilidad como herramienta de ayuda diagnóstica, con la capacidad de diferenciar y diagnosticar matemáticamente casos de enfermedad aguda, casos dentro de límites normales y en evolución.

Agradecimientos

Agradecemos a la Universidad Tecnológica de Pereira por su apoyo a nuestras investigaciones. Extendemos también nuestro agradecimiento al Centro de Investigaciones de la Clínica del Country, a la Doctora Adriana Lizbeth Ortiz, epidemióloga, y Silvia Ortiz, enfermera jefe, a la enfermera Sandra Rodríguez y a los Doctores Tito Tulio Roa, Director de Educación Médica, Jorge Alberto Ospina, Director Médico, y Alfonso Correa, Director del Centro de Investigaciones, por el apoyo a nuestro grupo de investigación.

Dedicatoria

A nuestros hijos.

18962

References

1. Devaney R (1992) A firstcourse in chaoticdynamicalsystemstheory and experiments. ReadingMass: Addison- Wesley.
2. Peitgen H, Jurgens H, Saupe D (1992) Chaos and fractals; new frontiers of science.:Springer, New York.
3. Calabrese JL (1999) Ampliando las fronteras del reduccionismo. Deducción y sistemas no lineales. RevPsicoan 2: 431-453.
4. Sánchez N, Ortiz W, Guzman S, Garduno MR (2008) Los límites del pronóstico newtoniano y la búsqueda del orden en el caos. IngenInvestTecnol 9: 171-181.
5. Mandelbrot B (1967)HowlongIsthecoastof britain? Statisticalself-similarityand fractionaldimension. Science 156: 636-638.
6. Goldberger AL, Rigney DR, West BJ (1990) Chaos and fractals in human physiology. Sci Am 262:42-49.
7. Bassingthwaighte JB, Liebovitch LS, West BJ (1994) Fractal physiology. Oxford UniversityPress, New York.
8. Weibel ER (1991) Fractal geometry: a designprinciplefor living organisms. Am J Physiol 261:L361-L369.
9. Abboud S, Berenfeld O, Sadeh D (1991)Simulation of high-resolution QRS complexusing a ventricular modelwith a fractal conductionsystem. Effects of ischemiaonhigh-frequency QRS potentials. Circ Res 68:1751-1760.
10. Nichols M, Townsend N, Scarborough P, Rayner M (2014) Cardiovascular disease in Europe2014: epidemiologicalupdate. EurHeart J 35: 2950-2959.
11. Mozaffarian D, Benjamin E, Go AS, Arnett DK, Blaha MJ, et al. (2015)Heartdiseaseand stroke statistics-2015 update. A reportfromtheamericanheartassociation. Circulation 131:e29-e322.
12. WHO.Theatlas of heartdiseaseand stroke. Deathsfromcoronaryheartdisease.
13. Organización Mundial de la Salud (2015) Centro de prensa. Enfermedades cardiovasculares
14. Pineda M, Matiz H, Rozo R (2002) Enfermedad coronaria. Editorial Kimpres Ltda., Bogotá.
15. Organización Mundial de la Salud (2012) Estadísticas sanitarias mundiales 2012.
16. Barron H, Viskin S (1998)Autonomicmarkers and prediction of cardiacdeathaftermyocardialinfarction. Lancet 351: 461-462.
17. Gómez M, Enciso C, Peña T, Segura Durán OD, Nieto Estrada VH (2012)Ecaisstudy: inadvertent cardiovascular adverse events in sepsis. Med Intensiva 36:343-350.
18. Lavenda, Bernard H (1990) Orden y caos. Barcelona: Prensa Cientifica, 1990; pp: 28-37.
19. Mandelbrot B (2000)The fractal geometry of nature. Freeman. Barcelona: TusquetsEds SA, pp: 341-348.
20. Goldberger AL, Bhargava V, West BJ, Mandell AJ (1986)Someobservationsonthequestion: Is ventricular fibrillation "chaos"?Physica D 19:282-289.
21. Goldberger A, Amaral L, Hausdorff JM, Ivanov P, PengCh, et al. (2002) Fractal dynamics in physiology: alterationswithdisease and aging. 99: 2466-2472.
22. Huikuri HV, Makikallio T, Peng CK, Goldberger AL, Hintze U, et al. (2000) Fractal correlationproperties of R - R intervaldynamics and mortality in patientswithdepressedleft ventricular functionafter and acutemyocardialinfarction. Circulation 101: 47-53.
23. Rodríguez J (2011)Mathematicallaw of chaoticcardiacdynamic: Predictions of clinicapplication. J MedMedSci 2:1050-1059.
24. Rodríguez J, Correa C, Melo M, Domínguez, D, Prieto S, et al. (2013)Chaoticcardiaclaw: Developingpredictions of clinicalapplication. J MedMedSci 4: 79-84.
25. Rodríguez J, Narváez R, Prieto S, Correa C, Bernal P, et al. (2013)Themathematicallaw of chaoticdynamicsappliedtocardíacarrhythmias. J MedMedSci 4: 291-300.
26. Guyton A, Hall J (2011)Organizació́n funcional del cuerpo humano y control del «medio interno». En: Guyton& Hall (Eds.) Tratado de fisiología médica. (12aedn.), Barcelona: Elsevier, pp: 3-10.
27. Crutchfield J, Farmer D, Packard N, Shaw R (1990) Caos. En: Crutchfield J, Farmer D, Packard N, Shaw R. Orden y caos. Scientific American. Prensa Cientifica SA, pp: 78-90.
28. Feynman R (1964) Comportamiento cuántico. En: Feynman RP, Leighton RB, Sands M Física. Wilmington: Addison-Wesley Iberoamericana, SA,pp: 37.
29. Feynman RP, Leighton RB, Sands M (1964) Leyes de la termodinámica. En: Feynman RP, Leighton RB, Sands M. Física. Wilmington: Addison-Wesley Iberoamericana, SA, pp: 44.1-44.19.
30. Tolman R (1979)Principles of statisticalmechanics. Dover Publications, New York.
31. Prieto S, Rodríguez J, Correa C, Soracipa Y (2014) Diagnosis of cervical cellsbasedon fractal and Euclidiangeometricalmeasurements: IntrinsicGeometricCellularOrganization. BMC Medical Physics 14:1-9.
32. Rodríguez J, Prieto S, Correa C, Dominguez D, Cardona DM, et al. (2015)Geometrical nuclear diagnosis and total paths of cervixcellevolutionfromnormalitytocancer. J Can Res Ther 11: 98-104.
33. Rodríguez J, Prieto S, Correa C, Bernal P, Puerta G, et al. (2010)Theoreticalgeneralization of normal and sickcoronaryarterieswith fractal dimensions and the arterial intrinsicmathematicalharmony. BMC MedPhys 10:1-6.
34. Rodríguez J, Prieto S, Correa C, Bautista J, Alejandro Velasco, et al. (2015)Mathematicsphysicalassessment of cardiacdynamicsbasedontheory of probability and proportions of entropy in theIntensivecareUnitforpatientswitharrhythmia. International Conferenceon Medical Phyiscs, Birmingham UK. J NuclMedRadiatTher 6:4.
35. Rodríguez J, Prieto S, Domínguez D, Melo M, Mendoza F, et al. (2013)Mathematical-physicalprediction of cardiacdynamicsusingtheproportionalentropy of dynamicsystems. J MedMedSci4: 370-381.
36. Rodríguez J, Prieto S, Bernal P, Izasa D, Salazar G, et al. (2015) Entropía proporcional aplicada a la evolución de la dinámica cardíaca. Predicciones de aplicación clínica. En: Rodríguez LG, Coordinador. La emergencia de los enfoques de la complejidad en América Latina: desafíos, contribuciones y compromisos para abordar los problemas complejos del siglo XXI. Tomo 1, (1aedn.), Buenos Aires: Comunidad Editora Latinoamericana,pp: 315-344.
37. Rodríguez J, Prieto S, Flórez M, Alarcón C, López R, et al. (2014)Physical-mathematical diagnosis of cardiacdynamicon neonatal sepsis: predictions of clinicalapplication. JMedMedSci 5: 102-108.
38. Rodríguez J, Prieto S, Correa C, Mendoza F, Weiz G, et al. (2015)Physicalmathematicalevaluation of thecardiacdynamicapplyingtheZipf-Mandelbrotlaw. J ModPhysics 6: 1881-1888.
39. Rodríguez J, Bernal P, Prieto P, Correa C, Álvarez L, et al. (2013) Predicción de unión de péptidos de Plasmodiumfalciparum al HLA clase II. Probabilidad, combinatoria y entropía aplicadas a las proteínas MSP-5 y MSP-6. Arch alergia inmunolclín 44: 7-14.
40. Correa C, Rodríguez J, Prieto S, Álvarez L, Ospino B, et al. (2012)Geometric diagnosis of erythrocytemorphophysiology: Geometric diagnosis of erythrocyte. J MedMedSci 3: 715-720.
41. Rodríguez J, Prieto S, Bernal P, Pérez C, Correa C, et al. (2012) Predicción de la concentración de linfocitos T CD4 en sangre periférica con base en la teoría de la probabilidad. Aplicación clínica en poblaciones de leucocitos, linfocitos y CD4 de pacientes con VIH. Infectio 16: 15-22.
42. Rodríguez J, Prieto S, Correa C, Perez C, Mora J, et al. (2013)Predictions of CD4 lymphocytes’ count in HIV patientsfrom complete bloodcount. BMC Medical Physics 13:3.
43. Rodríguez J (2010) Método para la predicción de la dinámica temporal de la malaria en los municipios de Colombia. RevPanam Salud Pública 27:211-218.
44. Rodríguez J, Correa C (2009) Predicción Temporal de la Epidemia de dengue en Colombia: Dinámica Probabilista de la Epidemia. Rev Salud pública 11: 443-453.
45. Rodríguez J (2015)Dynamicalsystemsappliedtodynamic variables of patientsfromtheintensivecareunit (ICU): Physical and mathematicalmortalitypredictionson ICU. J M edMedSci 6:209-220.