Key words
Multi-objective optimization, Evolutionary algorithms, Location modeling, GIS
Introduction
Ever-increasing population leads to a continuous rise of the demand for new health-care facilities. In every health-care facility planning problem, multiple criteria and objectives are involved. In many real-life situations, various objectives, particularly the environmental and economical objectives conflict with each other. Therefore, optimizing of a single objective may result in unacceptable solutions with respect to other objectives. As a result, in most of the location modeling problems, multiobjective optimization is necessary.
Generally, one of the essential spatial decision problems in urban applications is to search for optimal location(s) for one or more public facilities. The research literature in location modeling of health-care facilities is vast. Koutelekos et al., [1] determined the optimum location of medical centers in Thessaly region- Greece, by using Spatial Analysis of Geo-spatialinformation System (GIS). In Taiwan, Wu et al., [2] applied an Analytic Hierarchy Process (AHP)-based evaluation model for selecting optimal locations of hospitals. In their study, sensitivity analysis was performed by varying the objective factor decision weight, the priority weight of subjective factors and the gain factors. M.L. Burkey et al., [3] compared existing locations of health care services in four U.S. states with optimal locations satisfying two objectives: minimizing hospital- patient distance and maximizing the covering within a pre-specified time or distance. The customers travel from their own location to physicians and hospitals was considered in Chicago, USA and a simulation model was developed to evaluate the efficiency of hospital locations. [4] In a study in a rural district in Guatemala, a road network analysis was used to quantify access to health care services. [5] Locationallocation model for specialized health care services was solved using simulated annealing in USA [6]. Mitropoulos et al., [7] employed Data Envelopment Analysis (DEA) and Integer Programming (IP) to solve location allocation problem for health services in Greece. In another study in the Middle East, Ndiaye and Alfares, [8] applied a binary integer programming model to determine the optimal number and locations of primary health units for satisfying a seasonally varying nomadic population groups.
Facility location modeling is known as a Non- Polynomial (NP)-hard problem. [9] NP is a term of complexity in computer science which means solution can be determined in polynomial time by a non deterministic Turing machine. These problems cannot be easily solved using the traditional methods; especially when the location model includes various datasets and different criteria. Recently, heuristic algorithms have been used in most of the location problems. One of the most popular meta-heuristic methods, which have been widely and successfully used to solve the multi-objective location problems, is the Genetic algorithm (GA). GA is one of the global optimizing methods which can be used in large and nonlinear spaces. [9] As an example, Xiao et al., [10] applied multi-objective evolutionary algorithm to optimize the shape and location of sites by considering the cost surface in a raster model. A graph representation was used to encode the sites and evolutionary operators were used to improve the solution. In another study, Li et al., [11] used the ant colony optimization technique to solve the site selection problem by minimization of the total costs. Neema and Ohgai [12], presented a GA-based multi-objective optimization model to obtain optimum locations for urban parks and open spaces. They defined four objectives based on the Euclidian distance between the facility and demand points. Li and Yeh [9] integrated GIS and GA for searching the optimal locations in a continuous space.
On the other hand, integration of the Multiple Criterion Evaluation (MCE) methods with GIS can be used to find a single site or multiple sites sequentially. [13] GIS and MCE have been frequently used for site selection. [14-17] However, this approach may not be so useful for simultaneous optimization of the location of multiple sites, because in this situation, selection of one site may influence the suitability of the other alternative sites. Combination of MCE, GA and GIS can provide an interesting solution for simultaneous location of multiple facilities by considering multiple criteria, objectives and constraints, which have been applied in this study.
There are different types of health-care facilities such as the hospitals, clinics and urgent cars in urban areas. By considering the main requirements of the study area, optimization of the locations of the new clinics have been the main objective of this study. Combination of multi-objective (NSGA-II) and single-objective genetic algorithms has been used to solve the location-allocation problem for new clinics.
Materials and Methods
Multi-objective optimization problem
Many of the real life optimization problems deal with multiple objectives which conflict with each other, so that optimization with respect to a single objective may lead to inferior results with respect to the other objectives. The aim of multi-objective optimization methods is to find solutions where values of all the objective functions are as close to their optimum values as possible. To discover such solutions, a vector of decision variables should be found, so that the objective functions are optimized and constraints are satisfied.
Two general approaches have been applied for multi-objective optimization. In first approach, multi-objective optimization is converted to a single objective optimization. For example, in the weighted sum approach, a weight is assigned to each objective such that the sum of all weighted objectives forms a single objective problem. By using a single weight vector, only one solution is obtained. [18] In the second approach, an entire Pareto optimal solution set or a representative subset is determined. The solutions of a Pareto optimal set aren't dominated with respect to each other. The concept of dominance is used to compare two solutions a and b. If f (a) is no worse than f(b) in all of the objectives, and is better in at least one of them, then it is said that f(a) dominates f(b). The most important point in a multi-objective optimization is to find solutions of the Pareto optimal set. [18]
In general, in a priori approaches all knowledge about the relative importance of the objectives is required before starting the solving process. While in a posteriori approaches decision makers can choose the preferred solution from the set of Pareto-optimal solutions. [9]
Several survey papers have been published on GA-based multi-objective optimizations. Generally, multi-objective GA approaches differ by their fitness assignment procedures and elitism. [18]. One of the well-known multi-objective GA-based algorithms is NSGA-II which has been presented by Deb in 2002. [20] Because of its attractiveness, this algorithm has been used in this study to generate the multiple alternative solutions.
Description of the objective functions for healthcare settings location modeling
Fitness functions are defined according to the planning objectives. These functions indicate the suitability of solutions and play an important role for determination of the final results in evolutionary algorithms. In this paper, three planning objectives have been used for clinics location modeling as described below:
Minimization of the transportation costs
This objective function was defined to minimize the total transportation costs for all of the service users. Transportation costs are represented by summing the distance between the facility locations to the demand points weighted by the corresponding population. The multi objective problem of clinic site location was formulated as follows:
i: index of demand point
j: index of potential site
pj: Population in the point i
dij: Total distance between the demand point i and potential site j
Yij is 1, if patients at point i are served by a clinic at site j, and is 0 if not.
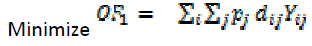 (1)
(1)
To meet this objective, a single-objective GA algorithm was used to optimize the allocation problem.
Minimization of the distance of sites to the roads
This objective function (OF2) was defined to minimize distances of the selected sites to the closest roads.
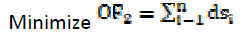 (2)
(2)
Where:
n is the number of the selected sites
dsi is the distance between the potential site i and the closest road.
OF2 was minimized by satisfying the minimum distance constraint between each pair of the selected sites.
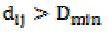 (3)
(3)
dij is the distance between the ith and jth potential sites
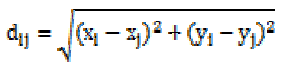
Dmin is the minimum allowed distance between each pair of sites for clinics
Maximization of distance from incompatible land uses
To minimize the negative effects of incompatible land uses on clinics, distances between the potential sites and these land uses were maximized.
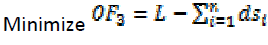 (4)
(4)
Where:
n is the number of the selected sites.
dsi is the distance between the site i and the closest incompatible land use with clinic.
L is a constant value
A multi-objective location-allocation model based on the genetic algorithm
The well-known multi-source Weber problem was solved by using the two related genetic algorithms (GAs). Genetic algorithms are special case of the more general class of evolutionary computation algorithms. Main stages of the proposed process are depicted in Fig. 1.
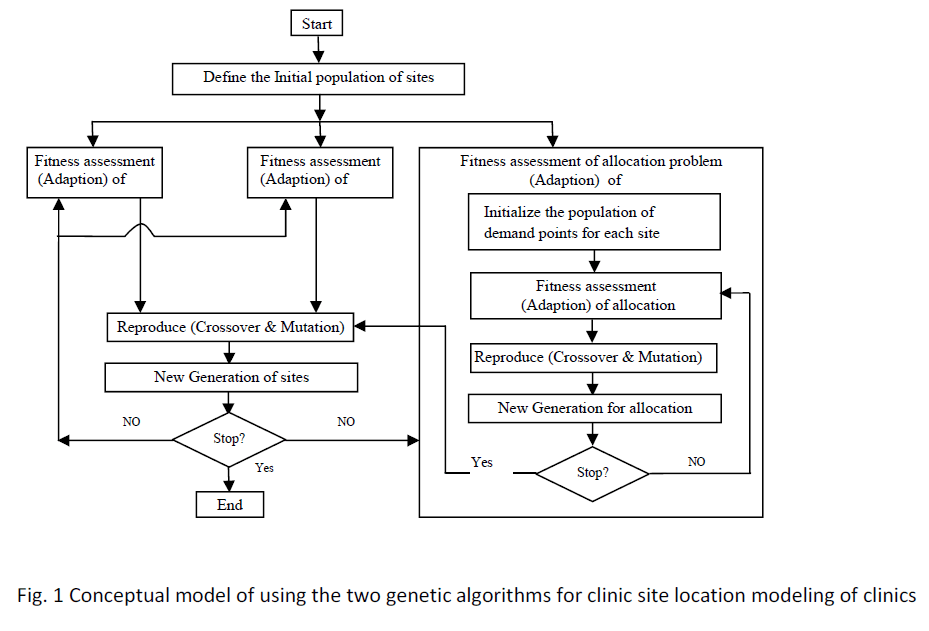
Figure 1: Conceptual model of using the two genetic algorithms for clinic site location modeling of clinics
In general, a GA consists of 5 steps: coding the problem, initialization of the population, definition of the evaluation function, definition of the genetic operators and determination of the parameters.
Location modeling of clinics was based on employment of two GAs including the external and internal GAs. If n is the number of required facilities and m is the number of candidate sites, every chromosome in the external GA consists of n genes. The value of each gene is an integer number between 1 to m which represents the site number.
The first objective (OF1) was defined to solve both the location and allocation problems. After selection of n sites in the first step, allocations of selected sites were optimized. This was done to minimize the weighted distances between the sites and demand points. To optimize the allocation, another genetic algorithm was used. In this internal GA, each chromosome includes p genes where p is the number of demand points. After minimization of the weighted distance, the best allocation of the selected sites was determined.
The least weighted distances were saved as the values of the first objective function for the selected sites and used as the fitness values of the sites chromosome.
Each chromosome of the external GA was also evaluated by the second and third objective functions.
To combine two parent chromosomes of sites (in external GA), a single point crossover was used. In allocation problem (internal GA) both the single point and two point crossovers were applied. It was assumed that the capacity of the facilities is not restricted.
A part of region 17 of Tehran urban areas is selected to practical test of the model. Population of the selected area is around 40000. At present, there is not a health-care facility in this area. If we suppose that each clinic can provide health services to 10000 people, four new clinics are required. GIS has been applied to analyze and organize relevant spatial data.
Datasets of different features including the parcels, streets, factories, industrial sites, stadium, gas stations and commercial centers were collected and used in the location planning process.
Map of parcels was used as the base map for determination of the alternative sites and definition of the demand locations. Whereas the possible locations for establishment of new clinics were limited in this area, 30 parcels were selected as the candidate sites.
Demand data were prepared by conversion of the parcels to points in ArcGIS software and consideration of the related population as the demand rate. Maps of the arterial and secondary streets were used to determine the accessibility of the sites. The alternative sites, parcels and streets of the study area are depicted in Fig. 2.
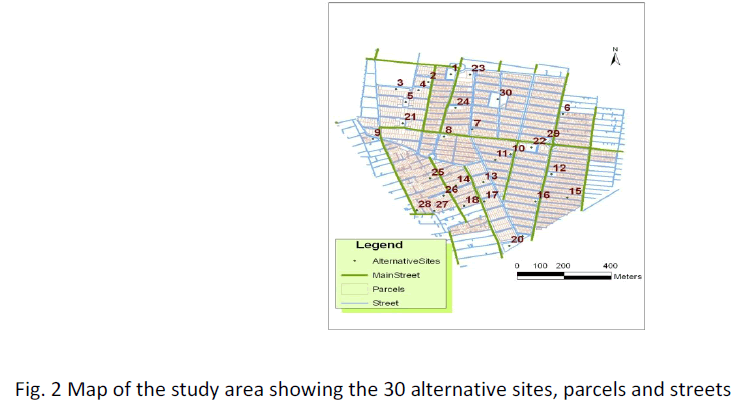
Figure 2: Map of the study area showing the 30 alternative sites, parcels and streets
A distance map was created by combination of all distances from each incompatible land use with clinics and used for optimization of the third objective function.
Results and discussion
After preparing the input data, the model was executed. Fifty solutions resulting from the multiobjective optimization using NSGA_II algorithm were investigated.
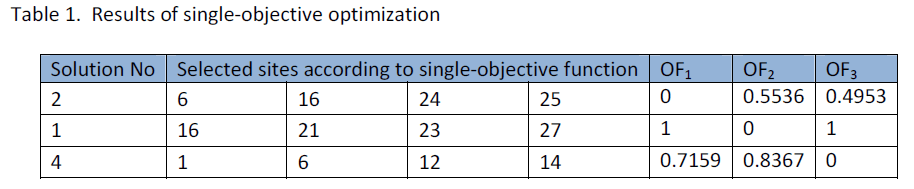
Table 1 presents the optimum solutions and related normalized values for each objective function.
Spatial location of the best solution for the first objective function (minimization of the total transportation costs) is depicted in Fig. 3. Second and third objective functions in this solution show medium scores. Service area of each site for 200 and 400 meters is also depicted in figure 3. These results show that by selecting the sites 6, 16, 24 and 25, the distance between most of the parcels to the nearest site is less than 400 meters.
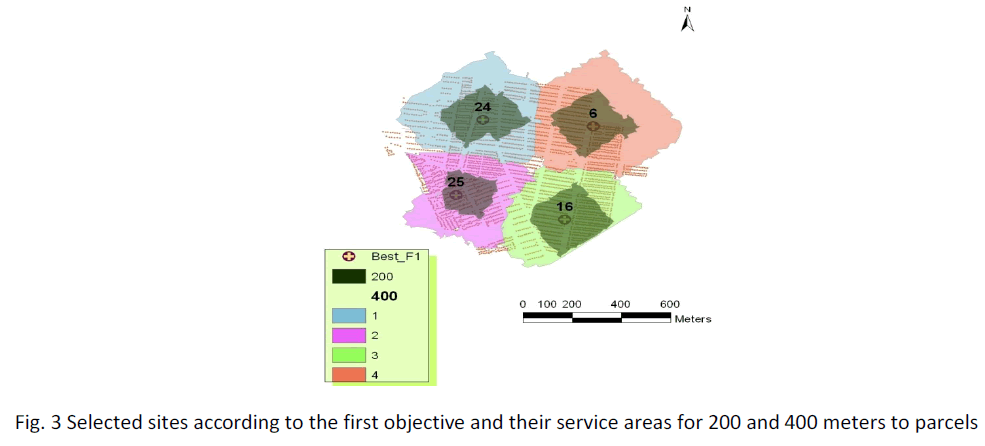
Figure 3: Selected sites according to the first objective and their service areas for 200 and 400 meters to parcels
The best solution according to the second objective function (the most accessible sites) is shown in figure 4(a).
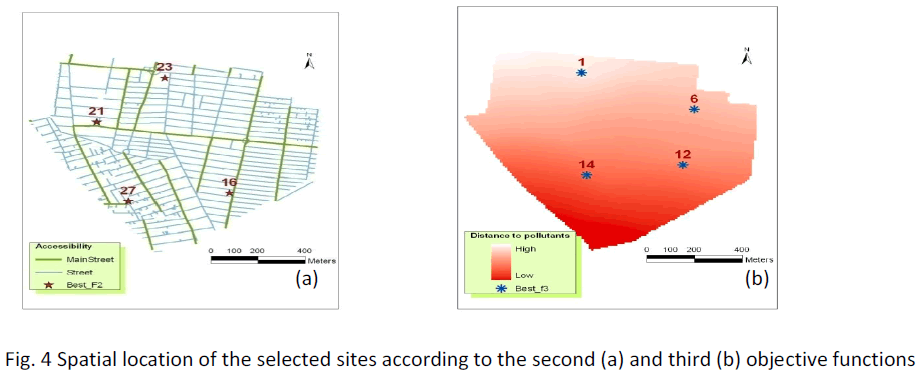
Figure 4: Spatial location of the selected sites according to the second (a) and third (b) objective functions
Shown in table 1, the best solution resulting from optimization of the second objective function, is the worst one among all of the solutions for the first and third objective functions. However site 16 is selected by optimizing the first and second objective functions.
Fig 4(b) depicts the best solution according to the third objective function (maximum distances from the incompatible areas).
The values of the first and second objective function are relatively high in this solution. Site 6 is selected in both solutions resulted from optimization of the first and third objective functions.
To compare the solutions, values of three objective functions were normalized. For each solution, normalized objective function values were added together (denoted by t). After sorting the solutions according to this value, ten solutions with the least values were selected and shown in Table 2. The normalized values of each objective function are represented in table 2.
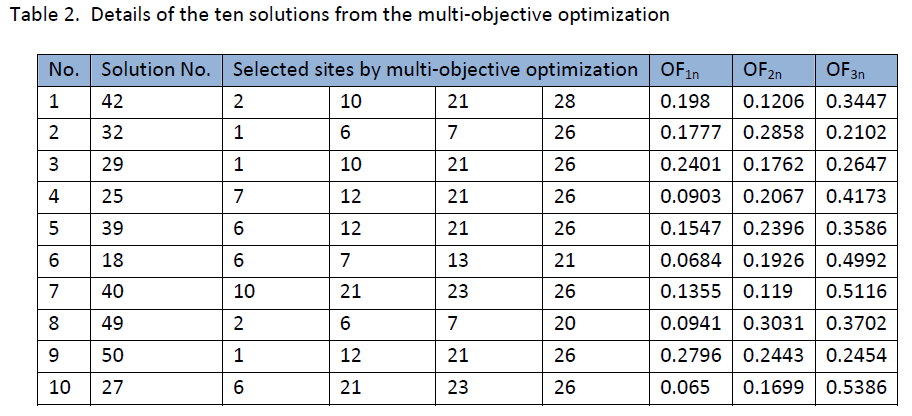
Although in solution number 42, all objective functions show relatively low values, this solution was not selected as the best solution in any of the three single-objective optimization tests.
In most of these ten solutions, third objective value is higher than other objective values. The total value (t) for solution numbers 42, 32 and 29 are close together.
Decision makers can select one best solution from the pool of non-dominated solutions according to their preferences. Relative importance of each objective can be considered as a weight vector to determine the best solution. For example if we consider the weight vector as w= [0.5 0.3 0.2], the solution number 25 will be the best one.
In this paper, a GA-based model has been proposed to search optimal locations for new clinics. Three objectives have been defined to determine the sites near the populated points and streets and far from the incompatible land uses.
The objectives were optimized by a multiobjective GA simultaneously to explore the nondominated Pareto optimal solutions. To solve the Location-Allocation problem, two related GAs were combined. One of them is a single-objective GA to allocate clinics according to the population and distances. The other one is a multi-objective GA to determine the optimal locations of new clinics according to the three objectives.
The proposed method has been tested in region 17 of Tehran urban areas. Computational results have shown that several optimum solutions can be acquired using this model so that different decision makers would be able to determine the relative importance of objectives based on their own preferences and select the best solution.
3021
References
- Koutelekos J, Photis NY, Milaka K, Bessa N, Manetos P. Primary Care Clinic Location Decision Making and Spatial Accessibility for the Region of Thessaly. Health science journal 2008; 2(1): 20-24.
- Wu CR, Lin CT, Chen HC. Optimal selection of location for Taiwanese hospitals to ensure a competitive advantage by using the analytic hierarchy process and sensitivity analysis. Building and Environment 2007; 42(3): 1431–1444.
- Burkey ML, Bhadury J, Eiselt HA. A location-based comparison of health care services in four U.S. states with efficiency and equity. Socio-Economic Planning Sciences 2012; 46(2): 157-163.
- Morrill RL, Schultz R. The transportation problem and patient travel to physicians and hospitals. Annals of Regional Science 1971; 5(1):11 -24.
- Owen KK, Obregón EJ, Jacobsen KH. A geographic analysis of access to health services in rural Guatemala. International Health 2010; 2 (2):143–149.
- Syam SS, Côté M. A location–allocation model for service providers with application ton ot-for-profit health care organizations. Omega 2010; 38 (3-4):157–166.
- Mitropoulos P, Mitropoulos I, Giannikos I. Combining DEA with location analysis for the effective consolidation of services in the health sector. Computers & Operations Research. 2012; In Press.
- Ndiaye M, Alfares H. Modeling health care facility location for moving population groups. Computers & Operations Research 2008; 35 (7): 2154 – 2161.
- LI X, YEH AG. Integration of genetic algorithms and GIS for optimal location search. International Journal of Geographical Information Science 2005; 19 (1): 581–601.
- Xiao N, Bennett DA, Armstrong MP. Using evolutionary algorithms to generate alternatives for multi-objective site-search problems. Environment and Planning A 2002; 34(4): 639-656.
- LI X, HE J, LIU X. Intelligent GIS for solving highdimensional site selection problems using ant colony optimization techniques. International Journal of Geographical Information Science 2009; 23(4): 399–416.
- Neema MN, Ohgai A. Multi-objective location modeling of urban parks and open spaces: Continuous optimization. Computers, Environment and Urban Systems 2010; 34 (5): 359–376.
- Carver SJ. Integrating multi-criteria evaluation with geographical information systems. International Journal of Geographical Information Systems 1991; 5(3): 321– 339.
- Sener S, Sener E, Nas B, Karagüzel R. Combining AHP with GIS for landfill site selection: A case study in the Lake Beysehir catchment area. Journal of Waste Management 2010; 30(11): 2037-2046.
- Tuzkaya G, Önüt S, Tuzkaya UR, Gülsün B. An analytic network process approach for locating undesirable facilities: an example from Istanbul. Journal of Environmental Management 2008; 88 (4): 970- 983.
- Vahidnia MH, Alesheikh AA, Alimohammadi A. Hospital site selection using fuzzy AHP and its derivatives. Journal of Environmental Management 2009; 90(10): 3048- 3056.
- Suárez-Vega R, Santos-Peñate DR, Dorta-González P, Rodríguez-Díaz M, A multi-criteria GIS based procedure to solve a network competitive location problem. Applied Geography 2011; 31(1): 282-291.
- Konak A, Coitb DW, Smithc AE, Multi-objective optimization using genetic algorithms. Reliability Engineering and System Safety. 2006; 91(9): 992–1007.
- Geoffrion AM, Dyer JS, Feinberg A, An Interactive Approach for Multi-Criterion Optimization, with an Application to the Operation of an Academic Department. Management Science 1972; 19 (4 Part 1): 357–368.
- Deb K, Pratap A, Agarwal S, Meyarivan T, A Fast and Elitist Multi-objective Genetic Algorithm: NSGA-II. IEEETransactions on Evolutionary computation 2002; 6(2):182 – 197.





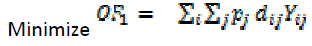 (1)
(1)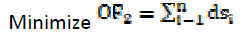 (2)
(2)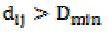 (3)
(3)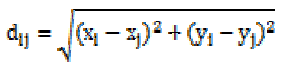
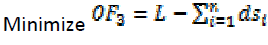 (4)
(4)




