Health Science Journal

Awards Nomination 20+ Million Readerbase

• JOURNAL HOME
• Editors
Articles
• In Process
• Archive
Authors
• Author Guidelines
• Submit Manuscript
In Detail
• Aim and Scope
• Publication ethics
• Peer Review Process
• Copyright
• Citations
• Special Issue
• Contact Us

Using hazard function approach in estimating the health and economic burden of COVID-19 in Delhi, India- in terms of Disability adjusted life years (DALYs) and Productivity loss

Sanya Aggarwal^1*, Sangeeta Chakravarty² and Gurprit Grover^{1 1}Department of Statistics, Faculty of Mathematical Sciences, University of Delhi, Delhi, India
²Institute of Economic Growth, Delhi University Enclave, Delhi, India
^*Correspondence: Sanya Aggarwal, Department of Statistics, Faculty of Mathematical Sciences, University of Delhi, Delhi, India, Email:

Received: 10-Oct-2023, Manuscript No. Iphsj-23-14157; Editor assigned: 12-Oct-2023, Pre QC No. Iphsj-23-14157(PQ); Reviewed: 10-Nov-2023, QC No. Iphsj-23-14157; Revised: 15-Nov-2023, Manuscript No. Iphsj-23-14157(R); Published: 22-Nov-2023

Keywords

Burden of disease; Disability adjusted life years (DALYs); Years of life lost due to disability (YLDs); Years of life lost (YLLs); Economic burden; Productivity loss

Abbreviations

DALY: Disability Adjusted Life Years; YLD: Years of Life Lost Due to Disability; YLL: Years of Life Lost Due to Death; YPPLL: Potential Years of Productive Life Lost; CPL: Cost of Productivity Lost; DW: Disability Weight; GDP: Gross Domestic Product

Introduction

Since the beginning of 2020, COVID-19 started as a global health emergency and evolved into a gigantic human and economic crisis across the globe. Till 30th April 2022, the COVID-19 pandemic in India has affected more than 43 million of population, second only to United States of America. India records a total death count of 0.52 million with the death rate of 433 per million population [1]. The spread of COVID-19 across the states in India has largely been askew. Delhi, which is a capital city of India, is second most populous city in the country after Mumbai [2]. High population density increases the risk of transmission leading to rise in daily infection rate [3]. About 4 percent of the total cases and 5 percent of the total deaths in India are reported from Delhi [4]. The death rate in the city is 1,559 per million of its population, only next to Maharashtra which records 2,067 deaths per million of its population.

To quantify high infection and death frequencies, mortality statistics such as case fatality rate, crude death rate, age specific death rate, etc. has widely been utilised. But these statistics are far from thoroughly comprehensive about the health status of the population, especially in different age groups. Greater social value is deemed to middle years of life as this population is likely to be looking after young and older people and the productivity level is highest during this age. Premature mortality in this age group thus inflicts consequential health and economic burden on the society of different magnitudes.

Some popularly used measure to assess the burden of disease are disability adjusted life years (DALY), potential years of productive life lost (YPPLL) and cost of productivity lost (CPL). DALY is used to measure the loss from living a shorter life from broad range of illness, adjusted for the severity of disease in individuals by their age, gender and premedical conditions [5,6]. DALY serves as an input in calculation of global burden of disease and as an output measure for the estimation of cost-effectiveness analysis [5]. It combines morbidity and mortality into a single index, in terms of years of life lost due to disability (YLD) and years of life lost due to premature mortality (YLL), respectively. On the other hand, YPPLL evaluates the loss incurred by the society in respect to individual’s productivity due to premature mortality in working age population [7,8]. The economic impact of mortality, in terms of value of labour productivity loss, in the working population is estimated through CPL [8].

In population level studies, the duration of illness and the remaining life expectancy are few of the major input parameters required for the estimation of DALY and YPPLL. Life expectancy at the age of death is generally extracted from the standardised life tables and sometimes from local life tables to maintain uniformity of results [9]. Duration of illness, on the other hand, is taken from the published medical sources. In case of steady state population, the duration of illness can be extracted from basic demographic identity that the prevalence of the disease is the product of incidence and duration of illness [10,11]. However, for general case no simple relationship exists between prevalence, incidence and duration [10].

Various studies have been conducted to estimate the burden of disease in India and around the world. The study by Nurchis et al. (2020) calculates DALY and productivity loss due to COVID-19 in Italy using parameters published by other studies [12]. Similar study has been conducted by John et al. (2021) in Kerala, India. Vasishtha et al. (2021) utilised data from multiple sources and the assumption that COVID-19 deaths are additional deaths in the population, measured the impact of infection on life expectancy, premature mortality and estimated DALY in Maharashtra, India [13]. Gökler & Metintaş (2022) estimated YLL and YPPLL in Turkey.

Premature deaths were calculated for men and women by interpolating the number of deaths and the expected life expectancy, whereas productivity loss was estimated using predetermined wage rates with the human capital theory [14]. George et al. (2021) used simple linear regression model between incidence, prevalence, and duration to assess the duration of COVID-19 disease in various Indian states [11]. Grover et al. (2021) estimated DALY lost among HIV patients in Delhi, India by utilising the concept of mean residual life in estimation of remaining life from disease after the end of the study. This estimate is in turn used to measure the total duration of disease [15].

There is a lack of studies related to estimation of duration of illness in case of population level data. The main purpose of this study is to present a method of calculating duration of illness for estimation of DALYs and productivity loss in discrete time series population level data by fitting parametric hazard function. Life expectancy at death in the absence of COVID-19 is estimated using published life tables. These estimates are further utilised in estimation of YPPLL and CPL to assess the burden of disease. In the next section, the detailed method for the estimation is provided. Results from the implementation of the method are then presented and thorough discussion is conducted. Finally, the limitations of the study and a comprehensive conclusion are provided.

Materials and Methods

Study population

Data for this paper is drawn from various publicly available sources. Data related to COVID-19 cases, recovery and death is taken from the official website of Government of Delhi, India from the period of 2nd March 2020 till 30th April 2022 [16]. For the construction of life tables, the report on abridged life tables by Sample Registration System (SRS), 2014-18 is utilised [17]. The population data of Delhi is acquired from the census 2011 and the workforce participation rates are taken from the 68th round of employment and unemployment report from Delhi planning division [2,18]. The distribution of COVID-19 cases and deaths by age-group are taken from various news articles, based on which the study period is divided into three time periods namely, 2nd March 2020-31st December 2020; 1st January 2021-30th November 2021 and from 1st December 2021 to 30th April 2022 [19-22]. The data was managed in excel and R software was utilised for all the calculations.

Disability Adjusted Life years (DALY)

DALY is a measure of burden of disease that was constituted to incorporate the impact of morbidity in a proportional manner with mortality [23]. In other words, DALY is the combination of present value of future years of lifetime lost through premature mortality and the present value of the adjustment to years of future lifetime to allow for the average severity of any mental or physical disability caused by a disease or injury [5,23,24]. Thus, DALYs are a measure of something lost rather than something gained, so reduction of DALYs lost is the major objective [5].Mathematically, DALYs are calculated as:

[DALY]_i=[YLL] _i+ [YLD] _i (1)

Where [YLL] is the years of life lost due to premature mortality in the age-group i, and [YLD] is the years of life lost due to disability for the itch age-group. YLD and YLLs are estimated by applying a discounting factor of 3%. Discounting provides an incentive for policymakers and practitioners to focus on health interventions that can be implemented right away for immediate benefit and avoid the bias of saving resources for future eradication programmes [9].

For the premature mortality, the number of years lost is counted up to the maximum life span. YLLs are estimated as the product of total deaths at a point of time and life expectancy at death in i^Th age group. Mathematically,

YLL=(KCe^ra)/[(r+β)] ^2

[e^(-(r+β)(L+a)) {-(r+β)(L+a)-1}-e^

(-(r+β)a) {-(r+β) a-1}]+ (1-K)/r (1-e^(-rL))

Where, k=age weighting modulation factor; C=constant; r=discount rate; a=age of death; β=parameter from the age weighting function; and L=standard expectation of life at age a. The estimation of YLDs, on the other hand, is the number of cases in ith age group multiplied by the total duration of illness till remission or death and severity index known as disability weight on a scale of 0 (perfect health) and 1 (Death). Mathematically,

YLD=DW {(KCe^ra)/[(r+β)] ^2

[e^ (-(r+β)(π+a))

{-(r+β) (π+a)-1}-e^ (-(r+β) a)

{-(r+β) a-+ (1-K)/(r)(1-e^(-rπ))} (3)

Where k=age weighting modulation factor; C=constant; r=discount rate; a=age of onset of disability; β=parameter from the age weighting function; π=duration of disability; and DW=disability weight. In this study we assume C=0,β=0,k=0 and r=0.03. The disability weight is borrowed from the study by Wiper (2021) with the weight of moderate to severe being 0.133 and for critical cases assuming that they die is 0.655 [25]. Life expectancy before COVID-19 is estimated from the abridged life tables as per the need of the study [17].

Then the mathematical form of YLLs and YLDs as per this study is as follows:

YLL=Σ_i [N_i/r (1-e^ (-rL))] (4)

Where N_i is the number of deaths in age group i, (i=1,2,…,n); r is the discount rate of 3% and L is the life expectancy at the age i of death.

YLD=Σ_(i,j) (M_i× [DW]_j×(1-e^(-rπ)))/r (5)

where, M_i is the number of infected cases in age group i, (i=1,2,… ,n); r is the discount rate of 3%; [DW] _(j)is the disability weight for j^ the category (j=1 for moderate level and 2 for critical) and π is the duration of illness till remission or death.

Years of potential productive life lost (YPPLL) and cost of productivity loss (CPL)

The economic losses due to premature mortality and absenteeism due to infection is calculated using years of potential productive life lost (YPPLL) and cost of productivity loss (CPL). The productivity losses are calculated for the individuals who are in the working age bracket, i.e., between 15 and 65 years of age, using human capital approach. This approach is one way of valuing the amount of time by which working life is reduced due to illness or premature death [25,26]. This work time lost is then valued using wages as the proxy measure of employee output, adjusted for the workforce participation rate. The time lost due to illness is calculated using YPPLL. It is estimated in the similar manner as YLL, with the difference that only working age population is included in the estimation. The mathematical form of YPPLL is as follows:

YPPLL=Σ_I (D_i×(1-e^(-rL_i)/r (6)

Here, D_i is the number of deaths at age i,(i=1,2,…,n); r is the discount rate and L_i is the number of productive years remaining at the i^th age of death. To calculate cost of productivity loss due to death, the YPPLL are simply multiplied with workforce participation rate and the market wage, which is assumed in our case, to be GDP (Gross Domestic Product) per capita of ₹4,01,982 [27]. Cost of productivity loss due to absenteeism on the other hand, is estimated as the product of number of infected cases, proportion of working population in that age group, total duration of illness and salary per week. Here the salary is estimated from GDP per capita of Delhi, which is assumed to be the income of the population. So, CPL is calculated as:

[CPL] _ (death)=Σ _k [YPPL] _k×p_k×GDP per capita] (7)

[CPL]_(absenteeism)=Σ_k [N_k×p_k×d×S] (8)

Here, p_k is the proportion of working population in kth age group (k=15-65 years); Nk is the number of infected cases; d is the average duration of illness and S is the salary per day calculated from the GDP per capita.

Duration of illness

The method of obtaining the average duration of illness from COVID-19 till remission or death is outlined below. To accomplish this, firstly the connection between epidemic model and survival functions is established. In survival analysis, hazard function is of interest rather than the probability density function as the hazard functions are more informative about the underlying mechanism of failure [28]. Also, it can be noted that cumulative hazard rate uniquely defines a distribution.

Suppose the lifetime T takes the discrete set of values {t_i}; i=1, 2, at which the COVID-19 infected cases move to removed state (either recovery or dead). Then the probability mass function of a discrete lifetime distribution can then be written as, M_i=Pr [[T=t_i],i=1,2,…]; where, T is a random variable representing the duration or sojourn time of the individuals remaining infected. The survival function, S_i, which is defined as the probability of surviving beyond age t is obtained as,

S_i=Pr [[T≥t_i],i=1,2,…] (9)

=Σ_(j≥t_i) M_j

Where,

M_i=S_i-S_(i+1),i=1,2,… (10)

The hazard rate is the conditional probability, defined as the probability of leaving infection state at time i given that the individual has remained infected until time i, i.e.,

h_i=(Number of individuals removed in (i,i+Δi))/(Number of individuals alive at the beginning of the interval×Δi)

In this study the number of individuals removed is estimated by combining the number of recovered and number of deaths. Mathematically, the hazard rate can be written as:

h_i=Pr [T=t_i]/Pr [T≥t_i] (11)

The cumulative hazard function is then simply the accumulated hazard until time i. For the continuous case,

H(t)=∫_0^t h(u)du=-ln⁡[S(i).]

In discrete case, summing the hazard rate h_i, is not equal to-ln S(i). Various authors have provided different forms of H (t) for discrete cases [28,29]. This study utilises the cumulative hazard rate defined by Cox/Oakes (1984, p. 15) as,

H (t)=Σ_(t_j<t) [ ln [1-h_(i-1) ]⁡] (12)

When h_i is small, then the relation becomes,

H (t)≈Σ_(t_j<t) h_i (13)

The study estimates the cumulative hazard rate from the data to which different distributions are fitted. The distribution that best fits the data is identified by using R2 value. From the selected distribution, the median survival time is estimated which is used as measure of duration of illness. In this study, Weibull distribution fits the data best with parameters (λ,γ) and its median duration of infection is given by (ln2)^(1/γ)/λ.

Sensitivity analysis

Two-way sensitivity analysis is a technique used in economic evaluation studies by varying the values of two input parameters simultaneously and studying the combined effect on the results. In this study different choices of disability weight and discount rate are considered. The notation used is DALY (dw1, dw2), where dw1 is the disability weight for moderate, dw2 for critical and r is discount rate. On the other hand, one-way sensitivity analysis is conducted on CPL by varying the discount rate of 3% to 2.5% and 3.5% and the impact on results is reported.

Results

Table 1 provides the descriptive summary of COVID-19 related infected, recovered and dead cases in Delhi for the complete length of the study. Since the onset of COVID-19 in Delhi, a total of 1,883,075 cases of infection have been reported in the city with the average of 2,384 cases per day.

Table 1. Summary of COVID-19 cases from 2nd March2020 to 30th April 2022.

The maximum number of cases reported in one day was 28,867. Out of the infected cases a total of 1,851,184 cases have recovered till 30th April, 2022 with the average of 2,343 cases recovered per day. On the other hand, a total of 26,175 COVID-19 infected cases have died during this period with the average deaths per day being 33 and maximum deaths reported in a single day were 448. 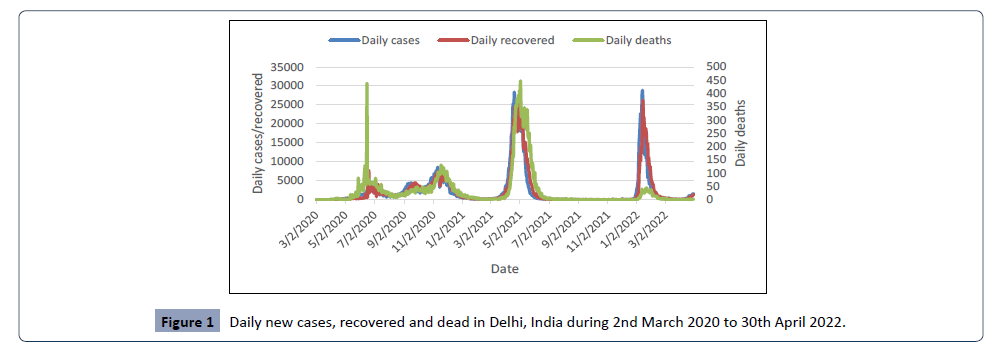However, as on 30th April 2022 about 5,716 are still infected with the virus, averaging at 13,619 cases active per day with minimum of one active case and peaking at 99,752 at a point of time. Figure 1 shows the trends of COVID-19 infection per day, where x-axis represents time in days, y-axis represents number of infection and recovery cases per day and secondary axis represents number of deaths per day.

Table 2 reports the R-square values of various distribution fitted to the cumulative hazard values. It is evident that Weibull distribution fits the data best with the R-square of 0.989. The parameters of Weibull distribution are estimated to be λ=0.02497 and γ=1.59743. Thus, the median survival time is obtained as 31.83 days. Table 3 lists the input parameters that are utilised in the estimation of DALYs and CPL. For the estimation of YLDs and hence DALYs, two disability weights were utilised. The disability weight of 0.133 was taken for the individuals that were infected and were able to recover and the weight of 0.655 was given to the individuals that died due to infection. Life expectancy at the age of death for the gap of 10 years is then constructed from abridged life tables and reported. The working age in India is 15 to 65 years. The proportion of population working in Delhi is extracted and presented in Table 3. A discount rate of 3% is applied for the estimation of both DALYs and CPL.

Table 2.Hazard distribution fitting and R-squared value

Table 3.Input parameters

Results

Since the first reported case till 31st December 2020, the overall burden of COVID-19 in Delhi was 1,82,420 DALYs at the discount rate of 3% (Table 4). About 7,658.9 healthy years of life were lost to the disability (YLD) and 1,74,760.9 years of total life was to premature death (YLL). The hefty share of DALYs was lost in agegroup 51-60 years with 46,521.5 years lost. It has been observed that out of the total YLDs lost; about 70% are lost in the age group of 50 years and below, whereas nearly 61% of YLLs share was reported in the age group of 51 years and above. This suggests that the disease was more fatal to older population. However, the DALYs lost per thousand cases during this period was 294.3 years, with majority loss of 779.2 years per 1000 cases in the age group of 71-80, followed by 770.1 DALYs lost per 1000 cases in age group 61-70 years. However,

Table 4. YLD, YLL and DALY (in years) estimates from March 2020- December 2020

The results of YLD, YLL and DALYs lost during 1st January 2021 till 30th November 2021 is reported in Table 5. The results show that about 2, 43, 827 DALYs was lost with a share of YLLs being 2,33,675.3 years and 10,152.8 years of YLDs. The maximum burden was observed in age group 51-60 years with a share of 26% in overall DALYs lost, whereas the rate of DALYs lost per thousand cases in the same age group was 562.2 years. The overall rate of DALYs lost per 1000 cases during this period was 297.1, with majority loss of 908.2 DALYs lost per 1000 cases in 71- 80 age group. It has been observed that about 70% of YLDs was lost till the age 50 years, whereas nearly 63% of YLLs share was reported in the age group of 51 and above. This suggests that the disease was more fatal to older population.

Table 5. YLD, YLL and DALYs (in years) estimates from January 2021 to November 2021

The results of burden of disease for the remaining period of five months from 1st December 2021 to 30th April 2022 are represented in Table 6. The gross discounted DALYs lost were 22106.5 years comprising a major share of 76.8% (16,999 years) of life lost to premature mortality (YLL). Highest burden was in the age group of 46-60 years with 6504.7 DALYs lost with 84% of the share of YLLs in total DALYs. The findings also suggest that more than half of the YLDs share to DALYs was contributed by the age group of 16-30 years. This age group also has the minimum life lost to mortality. It is to be noted that the total YLDs lost till the age of 45 years was 2.3 times higher as compared to YLDs lost in the age group above 45 years. On the hand, the ratio of YLLs below 45 years to above 45 years of age was 0.43, suggesting that the more YLLs were lost in the older age-group. The rate of DALYs lost per 1000 cases was 50.6 years with maximum rate in age group 76 and above (221.3 years per 1000 cases) and minimum in 16-30 years (21.3 years per 1000 cases).

Table 6. YLD, YLL and DALYs (in years) estimate from December 2021 to April 2022.

The combined DALYs lost during the total duration of the study are reported in Table 7. The gross loss in healthy years of life in terms of DALYs were 448341.7 years comprising of 425435.6 years lost to death (YLL) and 22906.4 years lost to disability due to infection (YLDs). The rate of DALYs lost per 1000 cases was 239 years with the minimum rate of 64 DALYs lost per 1000 cases in age group of below 30.

Table 7. YLD, YLL and DALYs (in years) estimates from March 2020 to April 2022.

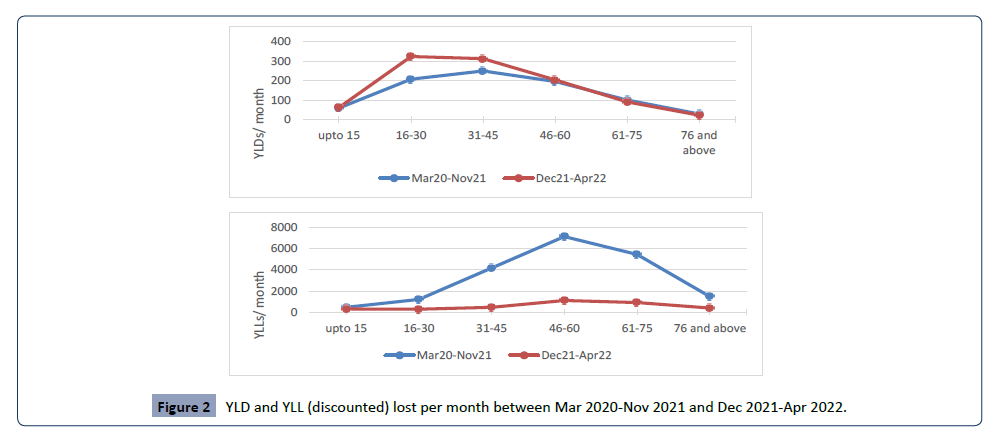
Figure 2 shows YLDs and YLLs lost per month during two time periods, namely, from March 2020 to November 2021 and December 2021 to April 2022. As can be seen from the graph, the YLDs lost per month were higher during the latter period till the age of 60 years. YLDs lost each month during the same period were 1.5 times higher than the former period. On contrary, more YLL per month were lost (in all age groups) till November 2021 as compared to the latter period. It is estimated the YLL lost per month in the age group of 46-60 years was 9 times higher till November 2021 as compared to the YLLs lost per month during the period of December 2020 to April 2022.

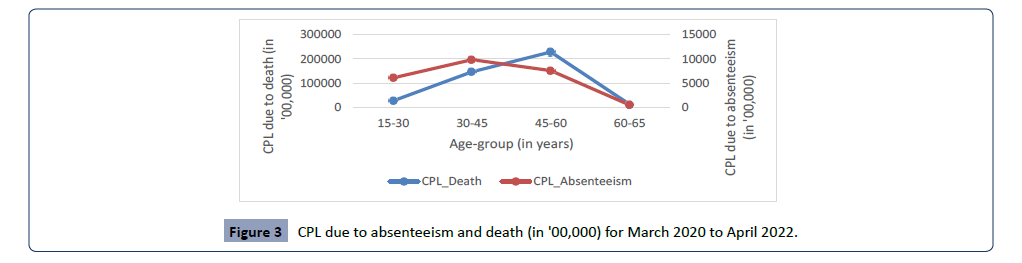
Productivity loss

In Delhi state of India, the total cost of productivity lost due to absenteeism from work was around ₹2.4 billion and due to premature death was about ₹41 billion during the complete duration of the study (Table 8). The majority of permanent loss was in the age group of 45-60 (₹22.8 billion) which also has the high burden of disease in terms of DALY. On the other hand, the major loss of productivity due to absenteeism from work was in age-group of 30-45 years (₹0.98 billion). The total productivity loss due to premature death and absenteeism are plotted in the Figure 3.

Table 8. Cost of productivity loss (CPL) due to morbidity (absenteeism) and pre-mature death (in rupees (₹).

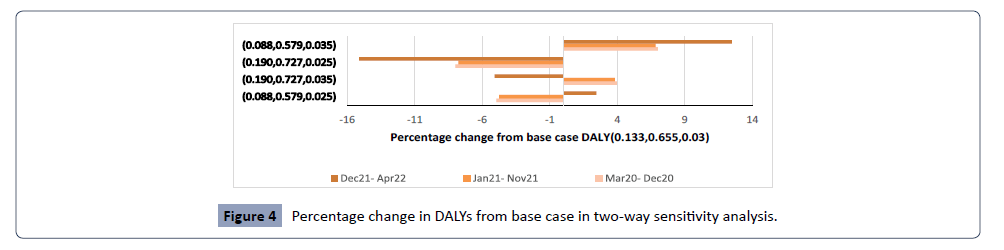
Table 9 reports the results of two-way sensitivity analysis on YLD, YLL and DALY estimation. The disability weight for moderate level is changed from 0.133 to 0.088 and 0.19, and for severe level the weight is changed from 0.655 to 0.579 and 0.727. Another input variable is discount rate which is adjusted to 0.025 and 0.035 from 0.03. The percentage change in DALY values from the baseline value of (0.133, 0.655, and 0.03) set at zero in four cases is presented in Figure 4.

Table 9. Sensitivity analysis on disability weight and discount rate of DALYs.

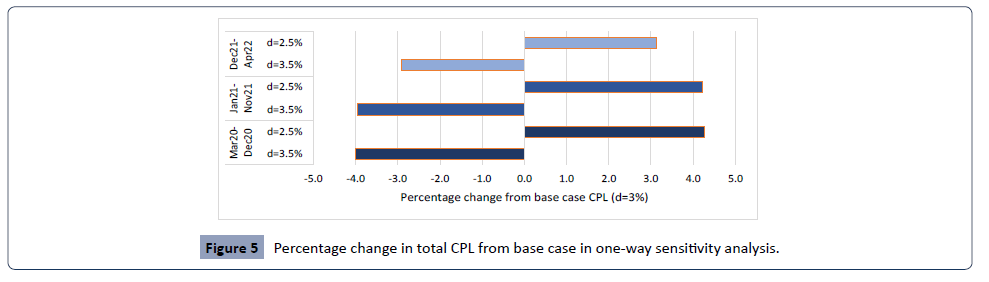
It is evident that major variation in the result is observed in the time period of December 2021 to April 2022 with the range of variation between-15% to 12%. The period of January 2021 to November 2021 shows the minimum variation ranging between-8% to 7% (Figure 4). Figure 5 represents the percentage in total productivity loss of from the baseline case of discount rate 3% to 2.5% and 3.5%. The results varied from-4% to 4.3% with minimum variation in the period of December 2021 to April 2022 from-2.9% to 3.1%.

Discussion

COVID-19 has shocked the institutions around the world. Despite of various containment measures, high infectivity with premature mortality and long-term morbidity has led to increased burden on limited healthcare resources, workforce shortages, economic loss as well as increasing psychological impact. Thus, analysing the burden of disease in terms of health loss and economic loss becomes imperative. In this context, the present study focuses on measuring the burden of COVID-19 disease in terms of DALYs and Cost of productivity loss in Delhi, India using hazard functions.

There are significant findings of this study. The period of infection follows Weibull distribution with median duration of illness, i.e., from the onset of infection till recovery or death, estimated to be 31.83 days. The result is in line with the report by WHO which states that the median duration for COVID-19 infection to resolve is about two weeks and for patients with severe or critical disease it takes three to six weeks. A study by Abrahim et. al., (2021) reports that the median duration of COVID-19 in Ethiopia was seven days with a minimum of two and a maximum of sixtyeight days. Thus, the findings suggests that in the absence of the medical records, the method employed in this chapter can provide an approximate value of the duration of illness from the disease.

The DALY estimates suggest that the burden of disease was mainly due to mortality with almost 95% of the contribution in DALYs is due to YLL. From the first inception of disease in city till 30th November 2021, three-fifth of the DALYs and YLLs were lost in age group of 50 and above, whereas, about 70% of the YLDs were lost in below 50 years of age. However maximum DALYs were lost during the period of 1st January 2021 to 30th November 2021. On the other hand, the DALY estimates for the period of 1st December 2021 to 30th April 2022 indicate that the even though YLL is the leading contributor in DALYs lost, about 23% of the disease burden was due to YLDs.

The findings also suggest that DALYs lost due to COVID-19 was highest among 51 to 60 years of age accounting for about 26% of the share in total DALYs lost. However, the rate of DALYs lost per 1000 cases was maximum in the age group 71 to 80 years. This means that the disease was fatal in older population of the Delhi especially in the age group of 71 to 80 years but more were infected in the age group of below 50 years. Similar results have been reported by other studies as well. A Study by Gökler & Metintaş (2022) in Turkey suggests that premature deaths were mainly in age group of 50-69 years [14]. Nurchis et al. (2020) stated that mortality was the main contributor in DALYs lost with the maximum burden in the age group of 70-79 years in Italy [12].

It has also been analysed that the majority of YLDs lost per month during the period of 1st December 2021 to 30th April 2022 in the age group of below 60 years are higher than YLDs lost in the period of 2nd March 2020 to 30th November 2021. Increase in YLDs can be attributed to the fact that the lockdown conditions during this period were relaxed with re-opening of schools, colleges and workplace, which in turn led to increased transmission. Another finding is that the YLLs lost per month were highest in period of 2nd March 2020 to 30th November 2021. This indicates that the share of mortality in overall disease burden was less during this time period. Reduced morality can be attributed to the vaccination drive in the country as the majority of population have been vaccinated in this period.

Further, the economic burden of COVID-19 in Delhi is estimated in terms of productivity loss which complements the health burden in the sense that about 95% of the productivity loss was due to mortality. It is observed that overall productivity loss due to mortality was 17 times higher than the loss due to absenteeism. Human capital approach was utilised for estimation of lost productivity due to mortality and absenteeism. It was estimated that more than half of the productivity loss due to mortality was in the working class of 45-60 years and two-fifth of the productivity loss was in the age group 30-45 years which was due to absenteeism. These estimates are alarming as the majority of the working population are in these age groups, with the participation rate of 60% in 45-60 years and 56.1% in 30-45 years. Even though the loss due to absenteeism was only 5% in total loss, it has huge impact on individual as well as society and in turn to economy as well. The results are in line with various studies as well [12,14].

In this process various assumption are undertaken which are the limitations of this study as well. The main limitation is that the average duration of infection for recovered and dead cases are not estimated separately due to limited availability of the data. This has led to under or overestimation of YLDs. But since YLDs have limited contribution in DALYs so this limitation can be eased. It is also assumed that the reinfection did not occur and the study is closed for birth, deaths and migrations. Impact of vaccination is also not taken in the study. The study thus does not provide a complete picture of the total burden of disease. Also, since the disease is patient specific and effects differently to different cases, the study is a population based and ignores patient level variation.

Conclusion

COVID-19 which started as a global health emergency has evolved into a gigantic human and economic crisis, placing substantial burden on limited healthcare resources across the globe. For population level studies, duration of illness is mostly derived from either medical records or through relationship between prevalence, incidence and duration of illness. The models presented in this study add to the existing literature of estimation of period of infection for population data that provides an approximate value of the duration of illness obtained from the medical records.

The result from this study suggests that severity of the disease was higher in older population which are more prone to other co-morbidities. The study puts light on burden of illness in age group of 15-30 years after the reopening of school, colleges and workplaces in Delhi. The study also suggests that during the earlier years of COVID-19 pandemic, the burden due to mortality in terms of YLL and CPL lost due to premature mortality was higher. With the course of time better control measures, medical preparedness and large coverage of vaccination, the burden due to mortality has been curtailed, increasing the burden on morbidity and loss due to absenteeism.

Measuring the disease burden in terms of health as well as economic loss is crucial for policy makers and nation as whole to understand the various strengths and limitation in the system and building better system to protect patients against future threat of disease.

References

1. Worldometer. COVID Live-Coronavirus Statistics 2022.
2. Census (2011) City census 2011, Registrar General of India, Ministry of Home Affairs, Government of India

Google Scholar

3. Chakravarty S, Grover G, Aggarwal S (2021) Association of Socioeconomic and Demographic Factors with COVID-19 Related Health Outcomes in SAARC Nations. Statistics and Applications, 367-386.

Indexed at, Google Scholar

4. Fox-Rushby J (2002) Disability-adjusted life years (DALYs) for decision-making an overview of the literature.

Google Scholar, Crossref

5. Vasishtha G, Mohanty SK, Mishra US, Dubey M, Sahoo U (2021) Impact of COVID-19 infection on life expectancy, premature mortality, and DALY in Maharashtra, India. BMC infectious diseases 21: 1-11.

Indexed at, Google Scholar, Crossref

6. Diaz-Jimenez D, Castaneda-Orjuela C, Castillo-Rodriguez L, De la Hoz-Restrepo F (2015) Economic costs analysis of the avoidable mortality in Colombia 1998–2011. Value in Health Regional Issues 8: 129-135.

Indexed at, Google Scholar, Crossref

7. Rumisha SF, George J, Bwana VM, Mboera LE (2020) Years of potential life lost and productivity costs due to premature mortality from six priority diseases in Tanzania, 2006-2015. 15: e0234300.

Indexed at, Crossref

8. Devleesschauwer B, Havelaar AH, Maertens de Noordhout C, Haagsma JA, Praet N (2014) Calculating disability-adjusted life years to quantify burden of disease. International journal of public health 59: 565-569.

Google Scholar

9. Alho JM (1992) on prevalence, incidence, and duration in general stable populations. Biometrics 587-592.

Indexed at, Google Scholar

10. George N, Tyagi NK, Prasad JB (2021) COVID-19 pandemic and its average recovery time in Indian states. Clin Epi and Global Health 1: 100740.

Indexed at, Google Scholar, Crossref

11. Nurchis MC, Pascucci D, Sapienza M, Villani L, D’ambrosio F (2020) Impact of the burden of COVID-19 in Italy: results of disability-adjusted life years (DALYs) and productivity loss. Int J Env Res public health 17: 4233.

Google Scholar, Crossref

12. John D, Narassima MS, Menon J, Rajesh JG, Banerjee A (2021) Estimation of the economic burden of COVID-19 using disability-adjusted life years (DALYs) and productivity losses in Kerala, India: a model-based analysis. BMJ open 11: e049619.

Indexed at, Google Scholar

13. Gokler ME, Metintas S (2022) Years of potential life lost and productivity costs due to COVID-19 in Turkey: one yearly evaluation. Public Health 203: 91-96.

Indexed at, Google Scholar, Crossref

14. Grover G, Chakravarty S, Aggarwal S, Deo V (2021) Estimating Disability Adjusted Life Years using Survival Models in HIV/AIDS Risk Groups. J Commun Dis 53: 36-47.

Indexed at, Google Scholar

15. Health & Family Welfare (2022) Covid 19 Related HFW Order. Health & Family Welfare-Covid 19 Related HFW Order.

Google Scholar

16. Office of the Registrar General and Census Commissioner, India (ORGI) (2019). Sample Registration System (Srs)-Abridged Life Tables 2014-2018.

Google Scholar

17. Government of NCT (2014). Employment & Unemployment situation in Delhi” based on 68th NSS round during 2011-2012.

Indexed at

18. Ghosh S (2020) 2,309 patients in 60-70 age groups died of COVID-19 in Delhi: RTI- the New Indian Express. The New Indian Express.
19. Statistia (2021) Number of the coronavirus (COVID-19) cases in India as of October 18, 2021, by age group.  

Google Scholar

20. Mathur A (2022) December-February: Every third Covid death in 61-75 age groups in Delhi. Times of India.
21. Ghosh S (2021) Toll maximum in 61-70 group in April-May killer wave- The New Indian Express.

Google Scholar

22. Murray CJL, Lopez AD (1996) the Global Burden of Disease. Cambridge, MA: Harvard School of Public Health; Harvard University Press.

Indexed at, Google Scholar

23. Donev D, Zaletel-Kragelj L, Bjegovic V, Burazeri G (2010) Measuring the burden of disease: disability adjusted life year (DALY). Methods and tools in public health 30:30.

Indexed at, Google Scholar

24. Wyper G, Assuncao R, Colzani E, Grant I, Haagsma JA (2021) Burden of disease methods: a guide to calculate COVID-19 disability-adjusted life years. Int J Pub Health 4.

Google Scholar

25. CREST. Cancer Research Economics Support Team (2016). Productivity losses and how are they calculated.

Indexed at

26. Delhi planning department Government of NCT of Delhi (2022). Economic survey 2021-2022.
27. Rinne H (2014) The Hazard rate: Theory and inference (with supplementary MATLAB-Programs).

Indexed at

28. KEMP AW (2004) Classes of discrete lifetime distributions; Comm. Statist. Theory & Methods 33, 3069-3093.

Google Scholar, Crossref

29. COX DR, OAKES D (1984) Analysis of Survival Data; Chapman & Hall, London.

Google Scholar