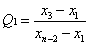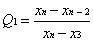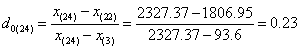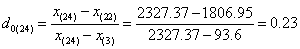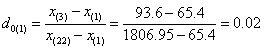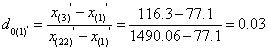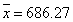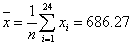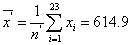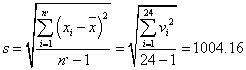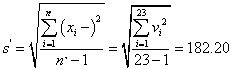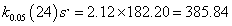Keywords
Average health care expense; Outlier detection; Grubbs’ test; Hampel’s test; Dixon’s test; T test
Introduction
Since the economic reform starting in the 1980’s, China’s economy has made remarkable achievements and the national per capita income has steadily increased [1]. At the same time, China's medical and health services have also made significant progress and improvement, but accompanied by a rapid increase of healthcare costs thus imposing heavy financial burden on Chinese residents [2]. As healthcare costs can have significant impact on the livelihood of the population, the reasons that lead to the rising healthcare costs have become the focus of attention for governments, health professionals, economists and even the general public worldwide. In China, healthcare costs have been witnessing yearly increase, but due to the financial crisis, wealth gap and regional differences, the rise in China’s per capita health care costs may have special contributing factors in some years. However, obvious regularity was not observed in the trend of increase to allow prediction. Recently, China’s per capita health care costs again rose rather rapidly in the past two years. In this context, we performed an analysis of the outliers of China’s per capita health care costs in the past years.
Outlier detection is a primary step in many data-mining applications. In the process of data analysis, we find that the dataset often contain some data that are substantially different from most of other data. These data are called outliers. Put it in another way, outliers mainly refer to the values that widely deviate from anticipation. In Social Economics and Statistics, any value showing an abnormal trend or inconsistency with the main data set would be considered as outliers. These outlier data may lead to the deviation of the data analysis results or errors. But from another perspective, these outliers may also be associated with some small probability events. The outliers may contain more than expected important information that warrant further investigation. There are many different methods in outlier detection [3]. In our current study, we selected Dixon’s test, T test, Grubbs’test and Hampel’s test to detect the outliers of China’s per capita health care costs from 1990 to 2013. These tests were chosen due to their simplicity over more complicated methods.
The objective was to select a relatively simple and accurate detection method that could assist the policy makers to ascertain deviation and improve prediction accuracy. This would contribute to policy research and analysis. In addition, when an outlier was detected, we also attempted to evaluate whether any factors or events could provide plausible explanation for the anomaly.
Methods
Data source
China Health Statistics Yearbook has a detailed statistical computation of China’s per capita health care costs over the years [4]. We chose China’s per capita health care costs from 1990 to 2013 for our current research. The specific data used is shown in Table 1.
| No. |
Year |
Per capital health care costs (Yuan) |
| X1 |
1990 |
65.4 |
| X2 |
1991 |
77.1 |
| X3 |
1992 |
93.6 |
| X4 |
1993 |
116.3 |
| X5 |
1994 |
146.9 |
| X6 |
1995 |
177.9 |
| X7 |
1996 |
221.4 |
| X8 |
1997 |
258.6 |
| X9 |
1998 |
294.9 |
| X10 |
1999 |
321.8 |
| X11 |
2000 |
361.9 |
| X12 |
2001 |
393.8 |
| X13 |
2002 |
450.70 |
| X14 |
2003 |
509.50 |
| X15 |
2004 |
583.90 |
| X16 |
2005 |
662.3 |
| X17 |
2006 |
748.80 |
| X18 |
2007 |
875.96 |
| X19 |
2008 |
1094.52 |
| X20 |
2009 |
1314.26 |
| X21 |
2010 |
1490.06 |
| X22 |
2011 |
1806.95 |
| X23 |
2012 |
2076.67 |
| X24 |
2013 |
2327.37 |
Table 1: Per capital health care costs.
As can be seen from the Table 1, China’s per capita health care costs shows a rising trend year by year for nearly two decades with no observable significant regularity in pattern nor fixed magnitude of increase. Therefore, there is a need to have a simple data processing and trend prediction tool to assist policy makers.
Outlier-test procedures and test results
Applying Grubbs’ test for outliers: Named after its author, Frank Grubbs, Grubbs’ test is based on a normal distribution of the data [5-7]. This detection method may be used only for small dataset (n<40), with the outliers detected one at a time and excluded.
Based on our data, we calculated the mean and standard deviation as:
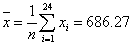
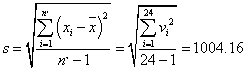
All data were then arranged in ascending order: x1=65.4<… x24=2327.37
As such, there were two possible outlier values in this dataset, but as the difference from the mean value was greater for x24 ( and
and  ) x24 was treated as a most likely outlier value. The g value for x24 was calculated as:
) x24 was treated as a most likely outlier value. The g value for x24 was calculated as:
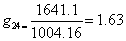
However, using α=0.05 as the significance level, g0.05(24)=2.644
As g24 value of 1.63was less than 2.644, x24 would have no gross error and should not be excluded.
The same approach was used to judge the remaining 23 data points, and these 23 numbers are arranged in ascending order. According to the result, these 23 numbers had no gross errors and should not be excluded.
Applying Hampel’s test of outliers
To calculate Hampel's test statistic, there is no need to use statistical tables. This method is not sensitive to outliers (i.e., quantity and value of outliers do not affect the results of Hampel’s detection), but it also does not require a large dataset [8,9].
In performing the Hampel's test, we needed to calculate the median (Me) of all data, the absolute residuals ri of each single data point from the median [ri=(xi-Me)], and the median of the absolute residuals( ). Any data point with ri>4.5
). Any data point with ri>4.5  would be considered as an outlier.
would be considered as an outlier.
For our dataset, the median (Me) was calculated as:
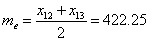
The absolute residuals (ri) of all data point from the median was presented in Table 2.
| Median ri |
Result |
| r1 |
356.8 |
| r2 |
345.1 |
| r3 |
328.6 |
| r4 |
305.9 |
| r5 |
275.3 |
| r6 |
244.3 |
| r7 |
200.8 |
| r8 |
163.6 |
| r9 |
127.3 |
| r10 |
100.4 |
| r11 |
60.35 |
| r12 |
28.45 |
| r13 |
28.4 |
| r14 |
87.25 |
| r15 |
161.6 |
| r16 |
240 |
| r17 |
326.5 |
| r18 |
453.7 |
| r19 |
672.2 |
| r20 |
892 |
| r21 |
1067 |
| r22 |
1067 |
| r23 |
1654 |
| r24 |
1905 |
Table 2: Absolute residual from the median (Hampel’s test of outliers).
Based on this, the median ( ) of the absolute residuals was calculated as 475.47. For our dataset, only data point (X24) had
) of the absolute residuals was calculated as 475.47. For our dataset, only data point (X24) had  , so X24 would be the outlier and should be excluded.
, so X24 would be the outlier and should be excluded.
Applying Dixon’s test of outliers
This method invented by Dixon has some limitations [10,11]. For example, only a large data set can be detected with this method. First data need to be arranged in ascending order for Dixon’s detection. Then the parameter Q (defined as gap/range) can be calculated for the suspected data point.
To detect whether the first data point in the data set is an abnormal value, the following formula can be used:
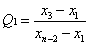
To detect whether the last data point in the data set is an abnormal value, the following formula can be used:
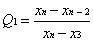
Where X1,2,3,n-2,n is the data in the data set.
If the calculated parameter Q > Qtable, where Qtable is a critical value corresponding to the sample size and confidence level, the data point can be regarded as an abnormal value.
For our data set, as n=24, we first tested x(1) and x(24),
According to the formula:
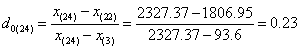

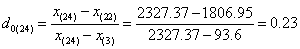
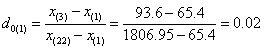
With the level of significance is set at 95% and n=24, a critical value of G0.05(24) = 0.413 was obtained from Dixon’s inspection coefficient table. Therefore, as the G values of x(1) and x(24) were less than 0.413, both were not outliers.
We arranged the remaining 24 data in ascending order, as shown in Table 3.
| Element |
Number |
One style |
Another style |
| X1 |
65.4 |
1 |
- |
| X2 |
77.1 |
2 |
1 |
| X3 |
93.6 |
3 |
2 |
| X4 |
116.3 |
4 |
3 |
| X5 |
146.9 |
5 |
4 |
| X6 |
177.9 |
6 |
5 |
| X7 |
221.4 |
7 |
6 |
| X8 |
258.6 |
8 |
7 |
| X9 |
294.9 |
9 |
8 |
| X10 |
321.8 |
10 |
9 |
| X11 |
361.9 |
11 |
10 |
| X12 |
393.8 |
12 |
11 |
| X13 |
450.7 |
13 |
12 |
| X14 |
509.5 |
14 |
13 |
| X15 |
583.9 |
15 |
14 |
| X16 |
662.3 |
16 |
15 |
| X17 |
748.8 |
17 |
16 |
| X18 |
875.96 |
18 |
17 |
| X19 |
1094.52 |
19 |
18 |
| X20 |
1314.26 |
20 |
19 |
| X21 |
1490.06 |
21 |
20 |
| X22 |
1806.95 |
22 |
21 |
| X23 |
2076.67 |
23 |
22 |
| X24 |
2327.37 |
24 |
23 |
Table 3: Data distribution for Dixon’s test.
We applied the same process to ,x (1) and ,x (24) , and obtained the following G values:

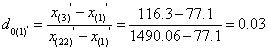
Based on n’=22, the critical value from the Dixon’s inspection coefficient table would be 0.421, again showing both were not abnormal values.
Applying T test for Outliers
For our data set, we first calculated the mean of the whole sample as:
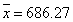
As X24 had the maximum residual from this mean, it was suspected as a potential outlier. To test this, we calculated the mean values and standard deviations as followed.
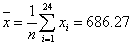
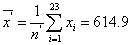
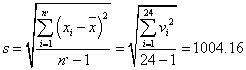
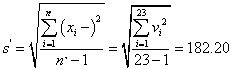
From the T test reference value table, k0.05(24) = 2.12 at the level of significance of 95%, we obtained:
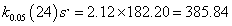
And x24 = 2327.37,
Hence, x(24) would be the outlier and should be excluded.
Summary of Test Results
We applied four outlier detection methods to the same dataset in our study, and the results showed the four methods possessed different outlier detection sensitivity. Based on Hampel’s and T tests, we found that data point x24 was the outlier and should be excluded. But both Grubbs’ and Dixon’s tests detected no outliers among these 24 values. The data
There are many outlier detection methods, such as Monte Carlo algorithms and data mining, etc. Although with high sensitivity in detecting outliers, all these methods require complicated computer models to perform the calculation, as well as much more stringent requirements. In contrast, the four methods used in our study only need simple data processing and calculation, but the sensitivity is relatively lower.
There are many outlier detection methods, such as Monte Carlo algorithms and data mining, etc. Although with high sensitivity in detecting outliers, all these methods require complicated computer models to perform the calculation, as well as much more stringent requirements. In contrast, the four methods used in our study only need simple data processing and calculation, but the sensitivity is relatively lower.
Relating factors and events to trend and outlier
According to the result, we concluded an abnormal value was observed for China’s per capita health care costs in 2013. This indicated that among the rising China’s per capita health care costs over the years, the curve fluctuated abnormally in 2013. Any abnormal change in the per capita health care costs would be closely associated with changes in many other factors affecting health care costs. In order to relate the anomaly (i.e. outlier value) observed in 2013 to events or factors that may cause the anomaly, we needed to examine what factors have been reported to affect health care costs in China and whether these factors (or events) were present around the time to cause the anomaly.
In a study using regression analysis and econometric model to analyze the impact of population aging on health care costs, Wang and Liu concluded that income levels, mortality and population aging rates were the major reasons leading to rising health care costs [12]. In another study, it was reported that economic growth and aging population were the main reasons leading to China’s per capita health care costs increase [13]. This finding was supported by the study by Li and He that showed the growth of China's health care expenses was mainly affected by economic growth [13]. However, this appeared to be a longrun relationship, and the short-term impact was not significant.
Compared to economic growth, the study also found health care price changes had little effect on China’s healthcare expenses.
Based on the findings of these studies, per capita health care costs showing a rising trend each year in China can be roughly attributed to the rise in per capita income and the increasing rate of aging population. Hence, when applied to evaluate any abnormal rise in per capita healthcare costs, the global economy and market environment, domestic economy and market conditions, and the degree of aging population would have an inseparable effect on the outliers. We would attempt to relate plausible events with the trend and abnormal value observed in 2013.
In 2008, the size of pension funds shrunk substantially around the world. Due to a high degree of linkage of capital markets, although not fully connected with the world's financial markets, this still had some impact on China’s capital market. In fact, at the end of 2007, China’s stock market began to fall, resulting in investment loss of many Chinese pension funds. As pension is an important financial source for of health care expenses, investment performance of pension funds would have a direct impact on China's per capita health care costs. Hence, China’s per capita health care costs began to experience slower rate of increase in 2007. And this did not improve in 2008 as China was facing the risk of high inflation. In 2009, with the recovering global economy, China’s capital investment market gradually expanded, which made up the investment losses of China’s pension funds and the total pension funds also increased significantly. The curve of per capital health care costs began to rise
In 2012, the outbreak of the international financial crisis had a profound impact on China’s financial and health care markets, resulting in stock market shrinkage and high unemployment. This also led to the decline in health care expenses. However, in 2013, China's aging population reached a new peak which affected the supply and demand of China’s health care market and the distribution of the national economy, thus causing another upturn in per capita healthcare costs.
In ending, as a limitation to our current study, we did not perform any factor & cluster analysis of the outliers in order to establish whether there underlying commonalities among groups and sub-groups of variables, and measurements within each. The main reason was that this study primarily aimed at exploring the applicability of simple methods in small data sets. In addition, for our case, it was difficult to select related factors a priori. Nevertheless, from our study, we did find per capita drug costs, per capita GDP value, population aging data and mortality also showed abnormal trends in 2013, could be factors contributing to the outliers. So, we plan to evaluate the relationship between these factors and the outliers in detail in our next study.
Conclusion
We applied four simple outlier detection methods to China’s per capita health care costs. The approach could allow the detection of abnormal values (i.e., outliers) and we could relate events and factors to the observed trend and outlier. This showed that this approach could be used in policy analysis.
7056
References
- https://www.theguardian.com/news/datablog/2012/mar/23/china-gdp-since-1980
- Yip W, Hsiao W (2014) Harnessing the privatisation of China’s fragmented health-care delivery. Lancet 2014 384: 805-18.
- Hodge VJ, Austin J (2004) A Survey of Outlier Detection Methodologies. Artificial Intelligence 22: 85-126.
- National Bureau of Statistics of China. China Statistical Year Book 2014. China Statistics Press, Beijing, China.
- Grubbs F (1950) Sample criteria for testing outlying observations. Annals of Mathematical Statistics 21: 27-58.
- Ma CA (1994) Health Care Payment Systems: Cost and Quality Incentives.Journal of Economics and management Strategy 8: 93-112.
- Ben-Ga I (2010) “Outlier Detection”.In: Maimon O,Rockach L (eds)Data Mining and Knowledge Discovery Handbook: A Complete Guide for Practitioners and Researchers (2ndedn), Springer,Science+BusinessMeda, New York, USA 2010: 117-130.
- Manoj K, Sen thamaraiKannan K (2013) Comparison of methods for detecting outliers. International Journal of Scientific & Engineering Research 4: 709-714.
- Dixon WJ (1950) Analysis of extreme values. Annals of mathematics Statistics 21: 488-506.
- Dean RB, Dixon WJ (1951) Simplified Statistics for Small Numbers of Observations. Anal Chem 23: 636-638.
- Wang X, Liu GB (2003) An Empirical Study of Aging Population and Rising Health Care Costs. Journal of Chongqing Three Gorges University 6:30-32.
- He PP (2005) An analysis of factors contributing to the increase of China’s Medical Cost. Pacific Journal 10:25-31.
- He PP, Li LY (2008) Analysis of the Growth of China’s Medical Expenses. Statistics and Decision-making 13:74-76.





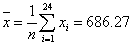
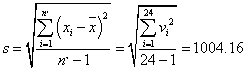
 and
and  ) x24 was treated as a most likely outlier value. The g value for x24 was calculated as:
) x24 was treated as a most likely outlier value. The g value for x24 was calculated as: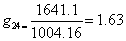
 ). Any data point with ri>4.5
). Any data point with ri>4.5  would be considered as an outlier.
would be considered as an outlier.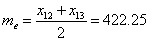
 ) of the absolute residuals was calculated as 475.47. For our dataset, only data point (X24) had
) of the absolute residuals was calculated as 475.47. For our dataset, only data point (X24) had  , so X24 would be the outlier and should be excluded.
, so X24 would be the outlier and should be excluded.